Unlock the secrets of exponentiation with a simplified explanation of 3 to the 6th power. Discover how to calculate this mathematical operation, and explore related concepts such as exponential growth, power functions, and bases. Learn how to apply this knowledge in real-world scenarios and improve your math skills with our easy-to-understand guide.
Understanding Exponents: A Beginner's Guide
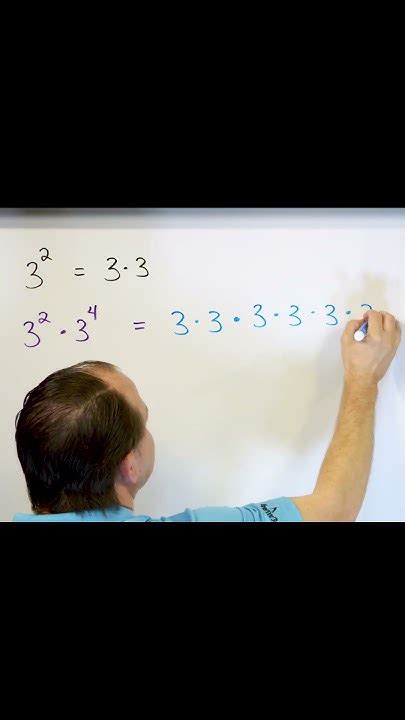
Exponents are a fundamental concept in mathematics, used to represent repeated multiplication of a number by itself. In this article, we will delve into the world of exponents, specifically exploring the concept of 3 to the 6th power. By the end of this article, you will have a clear understanding of exponents, how to calculate them, and their practical applications.
What are Exponents?
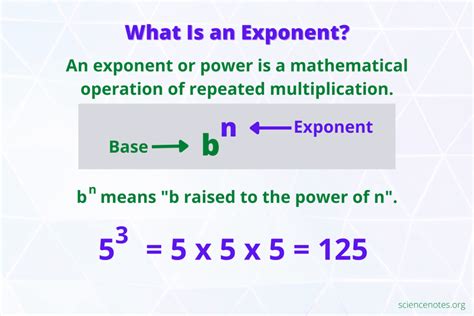
Exponents are shorthand for repeated multiplication. For example, 2^3 means 2 multiplied by itself 3 times, or 2 x 2 x 2 = 8. Exponents can be positive or negative, and they can be fractional or whole numbers. The base number is the number being multiplied, and the exponent is the power to which it is raised.
Understanding the Concept of 3 to the 6th Power
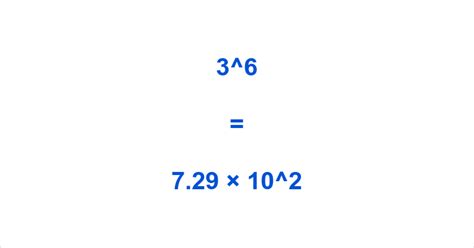
3 to the 6th power, denoted as 3^6, means 3 multiplied by itself 6 times. To calculate this, we can use the following steps:
- 3 x 3 = 9
- 9 x 3 = 27
- 27 x 3 = 81
- 81 x 3 = 243
- 243 x 3 = 729
Therefore, 3^6 = 729.
Practical Applications of Exponents
Exponents have numerous practical applications in various fields, including:
- Finance: Compound interest calculations use exponents to determine the future value of an investment.
- Science: Exponents are used to describe the growth of populations, chemical reactions, and physical phenomena.
- Computer Science: Exponents are used in algorithms for solving complex problems, such as cryptography and data compression.
- Engineering: Exponents are used to calculate stress, strain, and load on buildings and bridges.
Calculating Exponents with Different Bases
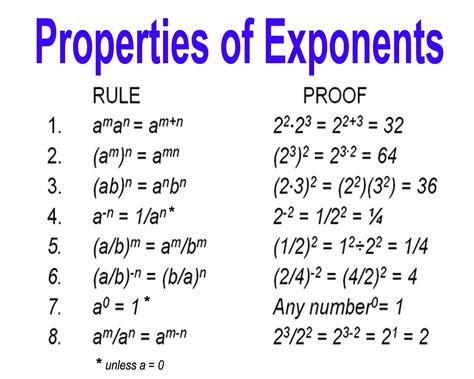
To calculate exponents with different bases, we can use the following rules:
- When multiplying exponents with the same base, add the exponents: 2^3 x 2^4 = 2^(3+4) = 2^7
- When dividing exponents with the same base, subtract the exponents: 2^5 ÷ 2^3 = 2^(5-3) = 2^2
- When raising an exponent to a power, multiply the exponents: (2^3)^4 = 2^(3x4) = 2^12
Common Mistakes to Avoid
When working with exponents, it's essential to avoid common mistakes, such as:
- Confusing the base and exponent
- Forgetting to evaluate the exponent before multiplying
- Not following the order of operations (PEMDAS)
Real-World Examples of Exponents
Exponents are used in various real-world applications, such as:
- Population growth: The population of a city can be modeled using exponents to predict future growth.
- Chemical reactions: Exponents are used to describe the rate of chemical reactions and the concentration of reactants.
- Computer networks: Exponents are used to calculate the number of possible connections in a network.
Conclusion: Mastering Exponents for Success
Mastering exponents is crucial for success in various fields, from finance to science and engineering. By understanding the concept of 3 to the 6th power and how to calculate exponents, you'll be better equipped to tackle complex problems and make informed decisions.
Exponents Image Gallery







FAQs:
- Q: What is an exponent? A: An exponent is a shorthand for repeated multiplication of a number by itself.
- Q: How do I calculate 3 to the 6th power? A: 3^6 = 3 x 3 x 3 x 3 x 3 x 3 = 729
- Q: What are some practical applications of exponents? A: Exponents are used in finance, science, computer science, engineering, and education.
We hope this article has helped you understand the concept of 3 to the 6th power and the importance of exponents in various fields. Share your thoughts and feedback in the comments section below!
