Admm Approximate Distance Method

The Approximate Distance Method, also known as ADM, is a technique used to estimate the distance between two points in a space. This method is particularly useful when dealing with complex systems or large datasets, where exact calculations can be computationally expensive or even impossible. In this article, we will delve into the world of ADM, exploring its importance, benefits, and applications in various fields.

The importance of distance calculations cannot be overstated. In many areas of science, engineering, and data analysis, understanding the distance between objects or points is crucial for making informed decisions or predictions. For instance, in navigation systems, accurate distance calculations are necessary for determining the shortest path between two locations. Similarly, in data clustering algorithms, distance measurements are used to group similar data points together. However, as the complexity of the system or the size of the dataset increases, exact distance calculations can become impractical. This is where the Approximate Distance Method comes into play.

The ADM is a heuristic approach that provides an estimate of the distance between two points, rather than an exact calculation. This method is based on the idea of approximating the distance between two points by using a subset of the available data or by employing simplifying assumptions. The resulting estimate may not be exact, but it can be computed much faster and with less computational resources. The trade-off between accuracy and computational efficiency is a key aspect of the ADM, and it has been widely adopted in various fields, including computer science, engineering, and statistics.

Introduction to Approximate Distance Method

The Approximate Distance Method has several benefits that make it an attractive choice for many applications. One of the primary advantages is its ability to handle large datasets and complex systems. By using approximations, the ADM can reduce the computational complexity of distance calculations, making it possible to analyze large datasets in a reasonable amount of time. Another benefit is its flexibility, as the ADM can be tailored to specific problems or domains. For example, in computer vision, the ADM can be used to estimate the distance between images or objects, while in natural language processing, it can be used to measure the similarity between text documents.

Key Concepts and Terminology

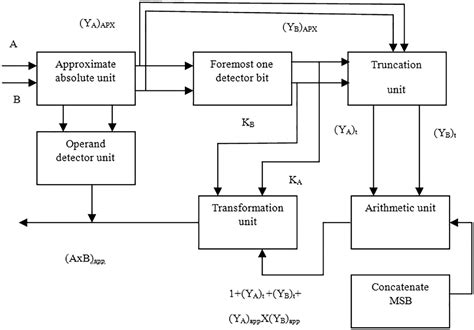
The ADM relies on several key concepts and terminology, including distance metrics, approximation algorithms, and heuristic search methods. Distance metrics, such as Euclidean distance or Manhattan distance, are used to define the distance between two points. Approximation algorithms, such as greedy algorithms or dynamic programming, are employed to estimate the distance between two points. Heuristic search methods, such as A\* search or best-first search, are used to explore the search space and find the approximate distance.

Applications of Approximate Distance Method

The Approximate Distance Method has a wide range of applications in various fields, including computer science, engineering, and statistics. Some of the key applications include:

• Data clustering and classification: The ADM can be used to estimate the distance between data points and group similar points together.
• Navigation and routing: The ADM can be used to estimate the distance between locations and determine the shortest path.
• Image and video processing: The ADM can be used to estimate the distance between images or objects and perform tasks such as object recognition and tracking.
• Natural language processing: The ADM can be used to estimate the similarity between text documents and perform tasks such as text classification and clustering.

Benefits and Limitations

The Approximate Distance Method has several benefits, including its ability to handle large datasets and complex systems, its flexibility, and its computational efficiency. However, it also has some limitations, including its potential for error and its reliance on simplifying assumptions. The accuracy of the ADM depends on the quality of the approximation algorithm and the distance metric used. Additionally, the ADM may not always provide the exact distance between two points, but rather an estimate that is close to the true distance.

Techniques and Algorithms

The Approximate Distance Method employs a range of techniques and algorithms to estimate the distance between two points. Some of the key techniques and algorithms include:

• Greedy algorithms: These algorithms make the locally optimal choice at each step, with the hope that it will lead to a global optimum.
• Dynamic programming: This technique breaks down complex problems into smaller sub-problems and solves each sub-problem only once.
• Heuristic search methods: These methods use heuristics, such as A* search or best-first search, to explore the search space and find the approximate distance.
• Approximation algorithms: These algorithms provide an estimate of the distance between two points, rather than an exact calculation.

Real-World Examples

The Approximate Distance Method has been used in a range of real-world applications, including: * Google Maps: The ADM is used to estimate the distance between locations and determine the shortest path. * Image recognition: The ADM is used to estimate the distance between images and perform tasks such as object recognition and tracking. * Text classification: The ADM is used to estimate the similarity between text documents and perform tasks such as text classification and clustering.

Future Directions

The Approximate Distance Method is a rapidly evolving field, with new techniques and algorithms being developed all the time. Some of the future directions for the ADM include:

• Improving the accuracy of the ADM: Researchers are working to develop more accurate approximation algorithms and distance metrics.
• Applying the ADM to new domains: The ADM has the potential to be applied to a range of new domains, including robotics, autonomous vehicles, and healthcare.
• Developing new techniques and algorithms: Researchers are working to develop new techniques and algorithms that can be used to estimate the distance between two points.

Conclusion and Summary

In summary, the Approximate Distance Method is a powerful technique that can be used to estimate the distance between two points in a space. The ADM has a wide range of applications in various fields, including computer science, engineering, and statistics. While it has some limitations, the ADM has the potential to be a game-changer in many areas, enabling faster and more accurate distance calculations.

Approximate Distance Method Image Gallery

We hope this article has provided you with a comprehensive overview of the Approximate Distance Method, its applications, and its future directions. If you have any questions or comments, please feel free to share them below. Additionally, if you found this article informative and helpful, please consider sharing it with others who may benefit from this knowledge.