Unlock the secrets of the pentagon with our comprehensive guide to angles inside a pentagon. Learn about the interior angles, exterior angles, and sum of angles in a pentagon, along with their properties and formulas. Discover how to calculate and use these angles in geometry and real-world applications.
The pentagon, a five-sided polygon, is a fascinating geometric shape that has been studied for centuries. One of the most interesting aspects of the pentagon is the angles inside it. In this article, we will delve into the world of angles inside a pentagon, exploring their properties, formulas, and applications.
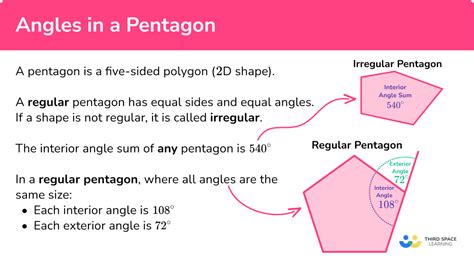
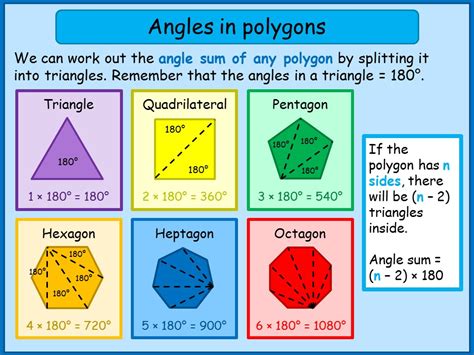
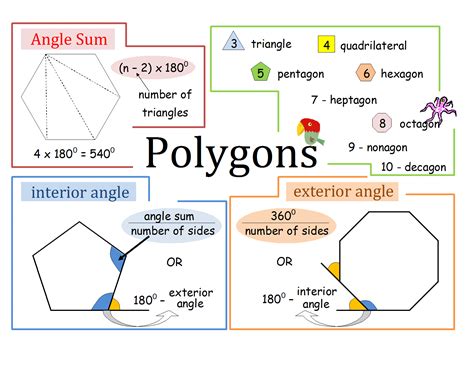
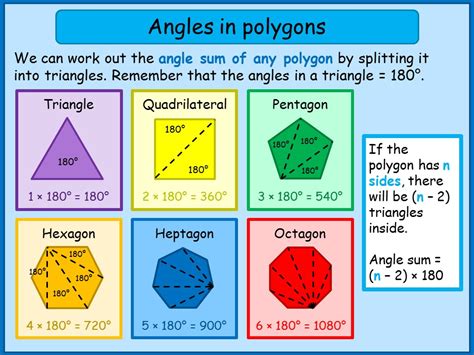
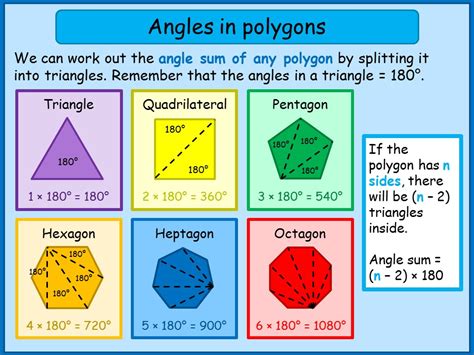
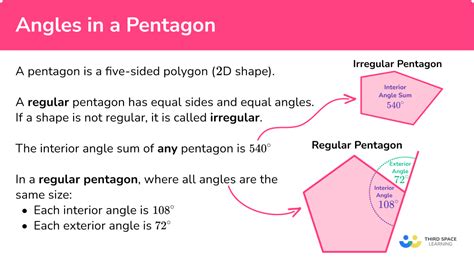
The sum of the interior angles of a pentagon is a fundamental concept in geometry. The formula for the sum of the interior angles of a polygon is (n-2) × 180°, where n is the number of sides. For a pentagon, which has five sides, the sum of the interior angles is (5-2) × 180° = 540°. This means that the sum of the angles inside a pentagon is always 540°.
Types of Angles Inside a Pentagon
There are several types of angles that can be found inside a pentagon, including acute angles, obtuse angles, right angles, and straight angles.
Acute Angles
An acute angle is an angle whose measure is less than 90°. In a pentagon, acute angles can be found at the vertices, where two sides meet. The sum of the measures of the acute angles inside a pentagon is always less than 540°.
Obtuse Angles
An obtuse angle is an angle whose measure is greater than 90°. In a pentagon, obtuse angles can also be found at the vertices, where two sides meet. The sum of the measures of the obtuse angles inside a pentagon is always greater than 90°.
Right Angles
A right angle is an angle whose measure is exactly 90°. In a pentagon, right angles can be found at the vertices, where two sides meet. The sum of the measures of the right angles inside a pentagon is always a multiple of 90°.
Straight Angles
A straight angle is an angle whose measure is exactly 180°. In a pentagon, straight angles can be found at the vertices, where two sides meet. The sum of the measures of the straight angles inside a pentagon is always a multiple of 180°.
Formulas for Angles Inside a Pentagon
There are several formulas that can be used to calculate the angles inside a pentagon. One of the most common formulas is the formula for the sum of the interior angles, which is (n-2) × 180°.
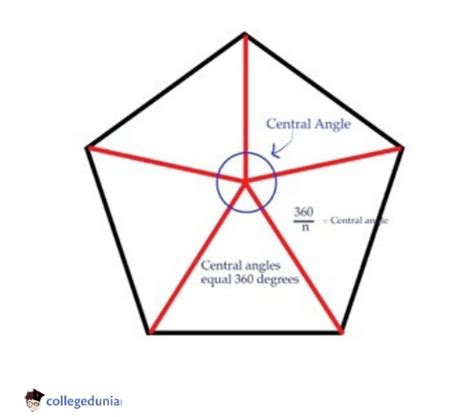
Another formula that can be used to calculate the angles inside a pentagon is the formula for the measure of each interior angle, which is 180° - (360°/n).
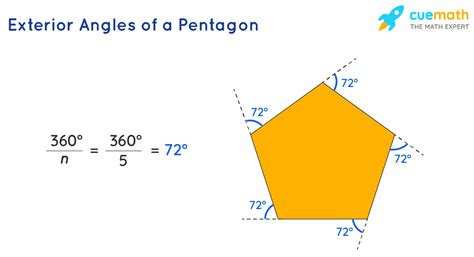
Applications of Angles Inside a Pentagon
The study of angles inside a pentagon has many practical applications in various fields, including architecture, engineering, and design.
In architecture, the study of angles inside a pentagon is used to design buildings and structures that are aesthetically pleasing and functional. For example, the ancient Greeks used the pentagon to design the Parthenon, one of the most famous buildings in history.
In engineering, the study of angles inside a pentagon is used to design and build bridges, roads, and other infrastructure. For example, the Golden Gate Bridge in San Francisco is a famous example of a pentagonal structure.
In design, the study of angles inside a pentagon is used to create visually appealing and functional designs. For example, the pentagon is used in graphic design to create logos, icons, and other visual elements.
Conclusion
In conclusion, the study of angles inside a pentagon is a fascinating and complex topic that has many practical applications in various fields. By understanding the properties and formulas of angles inside a pentagon, we can create aesthetically pleasing and functional designs that are used in architecture, engineering, and design.
Pentagon Angle Gallery
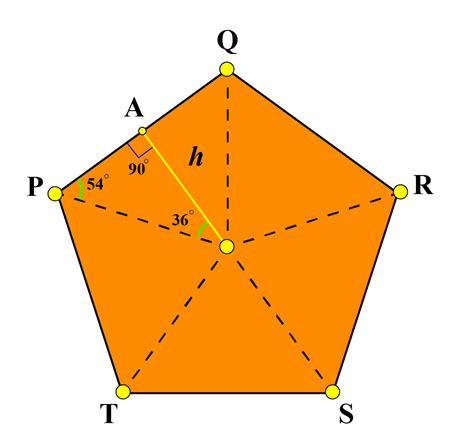
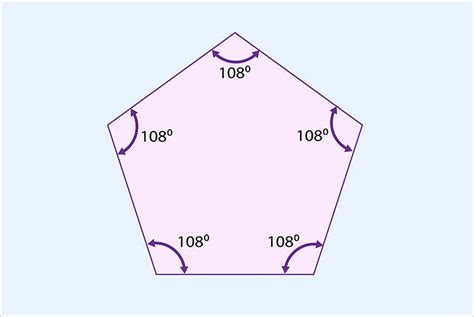
We hope this article has provided you with a comprehensive guide to angles inside a pentagon. Whether you are a student, teacher, or simply someone who is interested in geometry, we hope this article has been informative and helpful.
