Antiderivatives Of Inverse Trig Functions

The study of antiderivatives is a fundamental aspect of calculus, and when it comes to inverse trigonometric functions, the process can be quite complex. Inverse trig functions, such as arcsine, arccosine, and arctangent, are essential in various mathematical and real-world applications. Understanding how to find their antiderivatives is crucial for solving problems in physics, engineering, and other fields. In this article, we will delve into the world of antiderivatives of inverse trig functions, exploring their importance, working mechanisms, and providing practical examples to illustrate the concepts.

The importance of antiderivatives cannot be overstated, as they are used to solve a wide range of problems, from finding the area under curves to modeling the motion of objects. In the context of inverse trig functions, antiderivatives help us to find the definite integrals of these functions, which is essential in many applications. For instance, in physics, the antiderivative of the arctangent function is used to model the trajectory of projectiles. In engineering, the antiderivative of the arcsine function is used to design electronic circuits.

As we explore the world of antiderivatives of inverse trig functions, it is essential to understand the relationship between these functions and their derivatives. The derivative of an inverse trig function is used to find the rate of change of the function, while the antiderivative is used to find the accumulation of the function over a given interval. This relationship is crucial in understanding how to find the antiderivatives of inverse trig functions.

Introduction to Antiderivatives of Inverse Trig Functions

The antiderivatives of inverse trig functions can be found using various techniques, including substitution, integration by parts, and trigonometric substitution. Each technique has its own strengths and weaknesses, and the choice of technique depends on the specific problem and the level of complexity. For instance, the substitution method is useful for finding the antiderivative of the arcsine function, while integration by parts is useful for finding the antiderivative of the arctangent function.

Techniques for Finding Antiderivatives

The techniques used to find the antiderivatives of inverse trig functions are based on the properties of these functions and their derivatives. The following are some of the most common techniques used: * Substitution: This technique involves substituting the inverse trig function with a trig function, such as substituting arcsine with sine. * Integration by parts: This technique involves integrating one function while differentiating the other, such as integrating arctangent while differentiating the logarithmic function. * Trigonometric substitution: This technique involves substituting the inverse trig function with a trig function, such as substituting arctangent with tangent.

Antiderivatives of Specific Inverse Trig Functions

The antiderivatives of specific inverse trig functions, such as arcsine, arccosine, and arctangent, can be found using the techniques mentioned earlier. The following are some of the most common antiderivatives of inverse trig functions:

The antiderivative of arcsine: ∫arcsin(x) dx = x*arcsin(x) + √(1-x^2) + C
The antiderivative of arccosine: ∫arccos(x) dx = x*arccos(x) - √(1-x^2) + C
The antiderivative of arctangent: ∫arctan(x) dx = x*arctan(x) - (1/2)*ln(1+x^2) + C

Practical Examples

The antiderivatives of inverse trig functions have numerous practical applications in physics, engineering, and other fields. The following are some examples: * Finding the area under a curve: The antiderivative of the arcsine function can be used to find the area under a curve, such as the area under a parabola. * Modeling the motion of objects: The antiderivative of the arctangent function can be used to model the trajectory of projectiles, such as the motion of a ball thrown upwards. * Designing electronic circuits: The antiderivative of the arcsine function can be used to design electronic circuits, such as filters and amplifiers.

Benefits of Understanding Antiderivatives of Inverse Trig Functions

Understanding the antiderivatives of inverse trig functions has numerous benefits, including:

Improved problem-solving skills: Understanding the antiderivatives of inverse trig functions can help you solve a wide range of problems in physics, engineering, and other fields.
Enhanced mathematical knowledge: Understanding the antiderivatives of inverse trig functions can help you develop a deeper understanding of mathematical concepts, such as integration and differentiation.
Increased confidence: Understanding the antiderivatives of inverse trig functions can help you feel more confident when tackling complex mathematical problems.

Common Challenges and Solutions

When working with antiderivatives of inverse trig functions, you may encounter several challenges, such as: * Difficulty in finding the antiderivative: One of the most common challenges is finding the antiderivative of an inverse trig function, especially when the function is complex. * Difficulty in applying the antiderivative: Another common challenge is applying the antiderivative to solve a problem, especially when the problem involves multiple variables.

To overcome these challenges, you can use the following solutions:

Practice, practice, practice: The more you practice finding and applying antiderivatives of inverse trig functions, the more comfortable you will become.
Use online resources: There are many online resources available that can help you find and apply antiderivatives of inverse trig functions, such as online calculators and tutorials.

Gallery of Antiderivatives of Inverse Trig Functions

Antiderivatives of Inverse Trig Functions Image Gallery

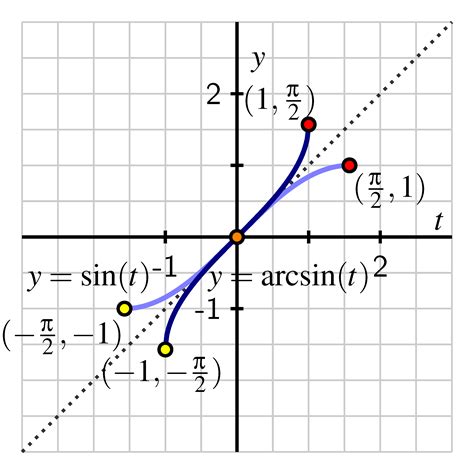
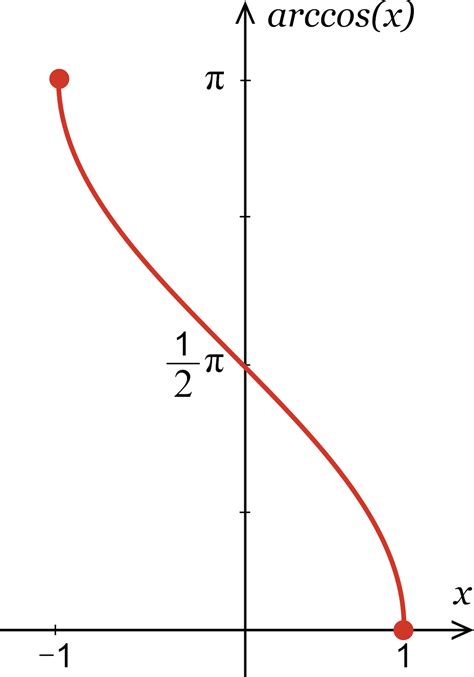
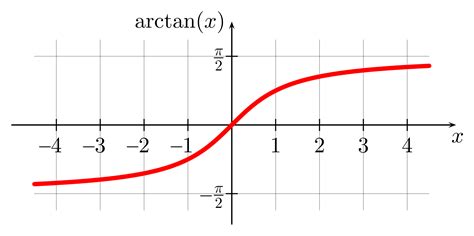
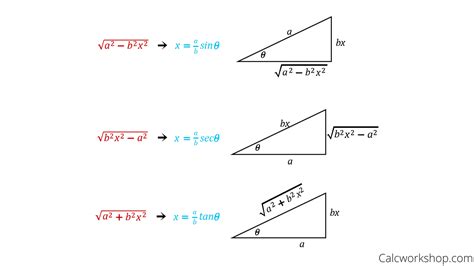
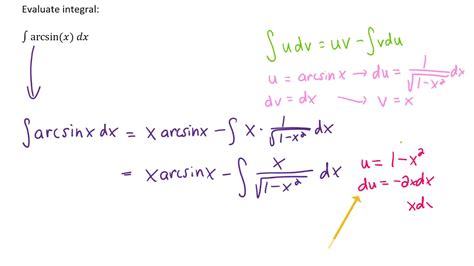
Final Thoughts

In conclusion, understanding the antiderivatives of inverse trig functions is essential for solving problems in physics, engineering, and other fields. By mastering the techniques of finding and applying antiderivatives of inverse trig functions, you can develop a deeper understanding of mathematical concepts and improve your problem-solving skills. We hope this article has provided you with a comprehensive understanding of the antiderivatives of inverse trig functions and has inspired you to continue exploring the world of calculus.

We invite you to share your thoughts and experiences with antiderivatives of inverse trig functions in the comments section below. Have you found this article helpful? Do you have any questions or topics you would like us to cover in future articles? Please don't hesitate to reach out and share your feedback. Additionally, if you found this article informative, please consider sharing it with your friends and colleagues who may benefit from this knowledge. Thank you for reading, and we look forward to hearing from you!