Irregular Pentagon Area Formula Calculator Made Easy

Calculating the area of an irregular pentagon can be a daunting task, especially for those who are not familiar with geometry. However, with the right approach and tools, it can be made easy. In this article, we will explore the concept of irregular pentagons, their properties, and provide a step-by-step guide on how to calculate their area using a formula calculator.

What is an Irregular Pentagon?

A pentagon is a five-sided polygon. When all the sides and angles of the pentagon are not equal, it is called an irregular pentagon. Unlike regular pentagons, irregular pentagons do not have any specific properties, making it more challenging to calculate their area.

Properties of Irregular Pentagons

Irregular pentagons have the following properties:

Five sides
Five angles
No equal sides or angles
The sum of interior angles is 540 degrees
The sum of exterior angles is 360 degrees

These properties can be used to identify and work with irregular pentagons.

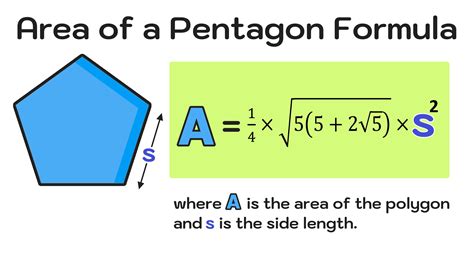
Calculating the Area of an Irregular Pentagon

Calculating the area of an irregular pentagon can be done using various methods, including the Shoelace formula, the Surveyor's formula, and the Divide and Conquer method. However, the most common and efficient method is the Shoelace formula.

The Shoelace Formula

The Shoelace formula is a mathematical algorithm used to calculate the area of a simple polygon, including irregular pentagons. The formula is:

Area = (1/2) * |(x1y2 + x2y3 + x3y4 + x4y5 + x5y1) - (x2y1 + x3y2 + x4y3 + x5y4 + x1y5)|

where (x1, y1), (x2, y2), (x3, y3), (x4, y4), and (x5, y5) are the coordinates of the vertices of the pentagon.

Using a Formula Calculator

To make the calculation easier, a formula calculator can be used. A formula calculator is a tool that allows you to input the coordinates of the vertices and calculate the area of the pentagon.

Here is an example of how to use a formula calculator to calculate the area of an irregular pentagon:

Suppose we have an irregular pentagon with the following coordinates:

(x1, y1) = (2, 3) (x2, y2) = (4, 5) (x3, y3) = (6, 2) (x4, y4) = (8, 4) (x5, y5) = (1, 1)

Using the Shoelace formula, we can calculate the area as follows:

Area = (1/2) * |(2 * 5 + 4 * 2 + 6 * 4 + 8 * 1 + 1 * 3) - (4 * 3 + 6 * 5 + 8 * 2 + 1 * 4 + 2 * 1)|

Area = (1/2) * |(10 + 8 + 24 + 8 + 3) - (12 + 30 + 16 + 4 + 2)|

Area = (1/2) * |(53) - (64)|

Area = (1/2) * |-11|

Area = 5.5

Therefore, the area of the irregular pentagon is 5.5 square units.

Benefits of Using a Formula Calculator

Using a formula calculator to calculate the area of an irregular pentagon has several benefits, including:

Accuracy: Formula calculators provide accurate results, eliminating the risk of human error.
Speed: Formula calculators are faster than manual calculations, saving time and effort.
Ease of use: Formula calculators are user-friendly, making it easy to input coordinates and calculate the area.

Common Applications of Irregular Pentagons

Irregular pentagons are used in various fields, including:

Architecture: Irregular pentagons are used in building design, particularly in the construction of roofs and walls.
Engineering: Irregular pentagons are used in the design of bridges, tunnels, and other infrastructure projects.
Computer graphics: Irregular pentagons are used in computer graphics to create 3D models and animations.

Conclusion

Calculating the area of an irregular pentagon can be challenging, but using a formula calculator can make the process easier and more accurate. By understanding the properties of irregular pentagons and using the Shoelace formula, you can calculate the area of any irregular pentagon. Whether you are an architect, engineer, or graphic designer, irregular pentagons play a crucial role in various fields, and being able to calculate their area is essential.