5 Essential Matrix Operations To Master

Matrix operations are a fundamental aspect of linear algebra and are used extensively in various fields, including physics, engineering, computer science, and data analysis. Mastering these operations is crucial for anyone who wants to work with matrices and understand their applications. In this article, we will explore five essential matrix operations that you need to master.

What are Matrix Operations?

Matrix operations are methods used to manipulate and transform matrices. These operations can be used to solve systems of linear equations, find the inverse of a matrix, and perform various other tasks. Matrix operations are essential in many fields, including physics, engineering, computer science, and data analysis.

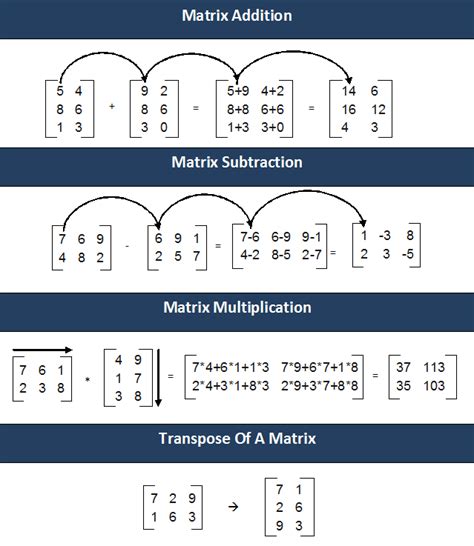
1. Matrix Addition

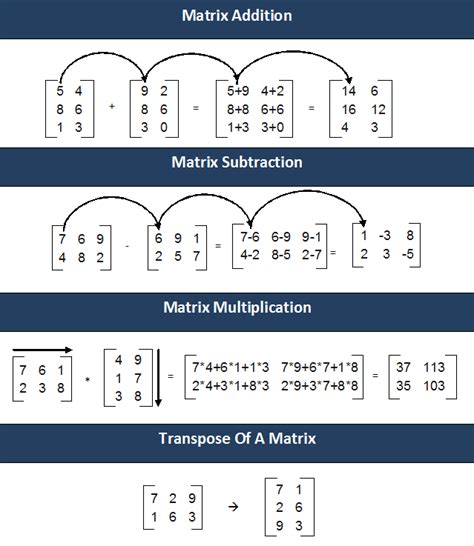
Matrix addition is one of the simplest matrix operations. It involves adding corresponding elements of two matrices. The resulting matrix has the same dimensions as the original matrices.

Rules for Matrix Addition

• The matrices must have the same dimensions.
• The corresponding elements of the matrices are added.
• The resulting matrix has the same dimensions as the original matrices.

Example:

A = | 1 2 | | 3 4 |

B = | 5 6 | | 7 8 |

A + B = | 6 8 | | 10 12 |

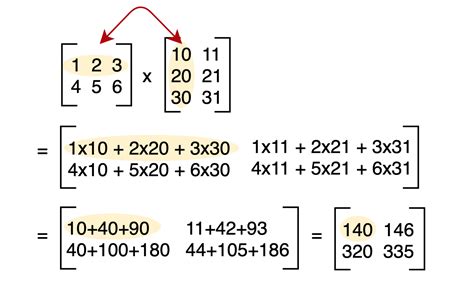
2. Matrix Multiplication

Matrix multiplication is a more complex operation than matrix addition. It involves multiplying corresponding elements of two matrices and summing the products. The resulting matrix has a different dimension than the original matrices.

Rules for Matrix Multiplication

• The number of columns in the first matrix must be equal to the number of rows in the second matrix.
• The corresponding elements of the matrices are multiplied and summed.
• The resulting matrix has a dimension equal to the number of rows in the first matrix and the number of columns in the second matrix.

Example:

A = | 1 2 | | 3 4 |

B = | 5 6 | | 7 8 |

AB = | 19 22 | | 43 50 |

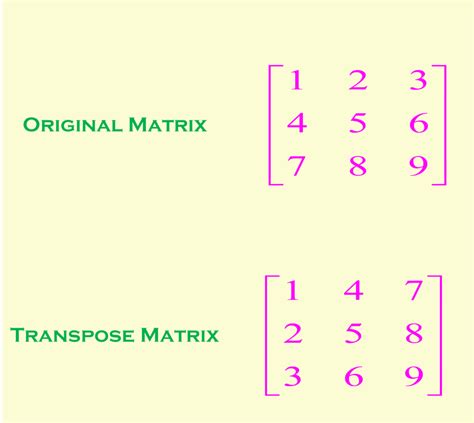
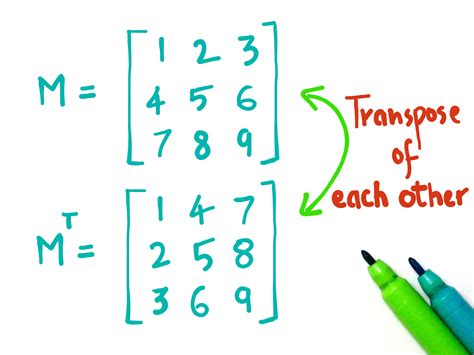
3. Matrix Transpose

The matrix transpose operation involves interchanging the rows and columns of a matrix. The resulting matrix has the same elements as the original matrix but with the rows and columns interchanged.

Rules for Matrix Transpose

• The rows and columns of the matrix are interchanged.
• The resulting matrix has the same elements as the original matrix.

Example:

A = | 1 2 | | 3 4 |

A^T = | 1 3 | | 2 4 |

4. Matrix Determinant

The matrix determinant operation involves calculating a scalar value that represents the scaling factor of a matrix. The determinant is used to find the inverse of a matrix and to solve systems of linear equations.

Rules for Matrix Determinant

• The matrix must be square.
• The determinant is calculated using a formula that involves the elements of the matrix.
• The resulting value is a scalar.

Example:

A = | 1 2 | | 3 4 |

det(A) = 14 - 23 = -2

5. Matrix Inverse

The matrix inverse operation involves finding a matrix that, when multiplied by the original matrix, results in the identity matrix. The inverse matrix is used to solve systems of linear equations and to find the solution to a matrix equation.

Rules for Matrix Inverse

• The matrix must be square.
• The matrix must have a non-zero determinant.
• The inverse matrix is calculated using a formula that involves the elements of the matrix.

Example:

A = | 1 2 | | 3 4 |

A^-1 = | -2 1 | | 1.5 -0.5 |

Matrix Operations Image Gallery

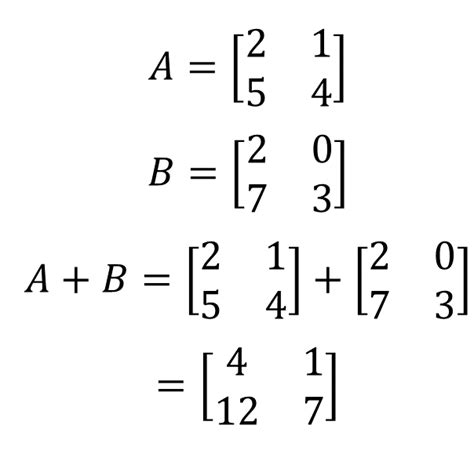
In conclusion, mastering matrix operations is essential for anyone who wants to work with matrices and understand their applications. The five essential matrix operations discussed in this article are matrix addition, matrix multiplication, matrix transpose, matrix determinant, and matrix inverse. By understanding these operations, you can perform various tasks, including solving systems of linear equations, finding the inverse of a matrix, and performing various other tasks.