Pricing options using binomial trees in Excel can seem daunting, but with the right approach, it can be made easy. In this article, we'll break down the process into manageable steps, providing you with a comprehensive guide on how to price options using binomial trees in Excel.
Understanding Binomial Trees
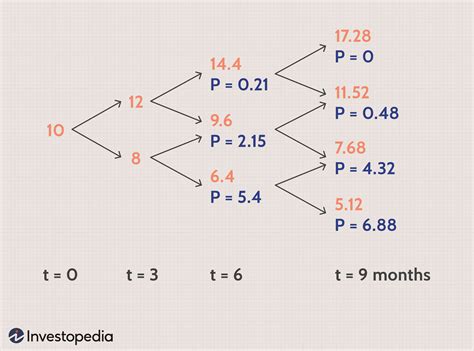
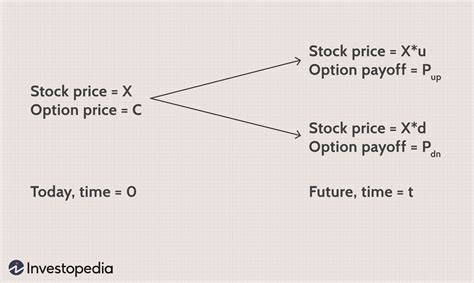
Before we dive into the Excel implementation, let's quickly review what binomial trees are and how they work. A binomial tree is a discrete-time model used to price options. It assumes that the underlying asset's price can only move up or down by a certain percentage at each time step. The tree is constructed by recursively applying the up and down movements to the asset's price, resulting in a lattice of possible prices.
Setting Up the Binomial Tree in Excel
To create a binomial tree in Excel, we'll need to set up a few inputs and formulas. We'll use the following inputs:
S: the current stock priceK: the strike price of the optionT: the time to expiration (in years)r: the risk-free interest rateq: the dividend yieldsigma: the volatility of the underlying assetn: the number of time steps
Inputs and Formulas
Create a new Excel sheet and set up the inputs as follows:
| Input | Value |
|---|---|
| S | 100 |
| K | 105 |
| T | 1 |
| r | 0.05 |
| q | 0.02 |
| sigma | 0.2 |
| n | 10 |
Next, we'll create the formulas to calculate the up and down factors, as well as the risk-neutral probabilities.
Up and Down Factors
The up and down factors are calculated using the following formulas:
Up factor (u): =EXP(sigma*SQRT(T/n))
Down factor (d): =1/u
Risk-Neutral Probabilities
The risk-neutral probabilities are calculated using the following formulas:
Probability of up movement (p): =(EXP((r-q)*T/n)-d)/(u-d)
Probability of down movement (1-p): =1-p
Constructing the Binomial Tree
Now that we have the inputs and formulas set up, we can construct the binomial tree. We'll use a separate sheet to create the tree.
Create a new sheet and set up the following headers:
| | 0 | 1 | 2 |... | n | | --- | --- | --- | --- |... | --- | | 0 | | | |... | | | 1 | | | |... | | |... | | | |... | | | n | | | |... | |
The first row represents the current time (t=0), and the first column represents the number of time steps (n). We'll fill in the tree recursively, starting from the current time and working our way backwards.
Filling in the Tree
The formula to fill in the tree is as follows:
=IF(COLUMN(A1)=1,S*(u^(ROW(A1)-1))*((1-p)^ROW(A1-1))*(p^(ROW(A1)-1-ROW(A1-1))),IF(COLUMN(A1)=n,S*(u^(n-1))*((1-p)^(n-1)),IF(ROW(A1)=1,S,IF(ROW(A1)=n,S*(d^(n-1)),IF(ROW(A1)>1,S*(u^(ROW(A1)-2))*((1-p)^(ROW(A1)-2))*(p^(ROW(A1)-2-ROW(A1-2))),S*(d^(ROW(A1)-2))*((1-p)^(ROW(A1)-2))*(p^(ROW(A1)-2-ROW(A1-2)))))))
This formula calculates the asset price at each node in the tree, using the up and down factors, risk-neutral probabilities, and the current asset price.
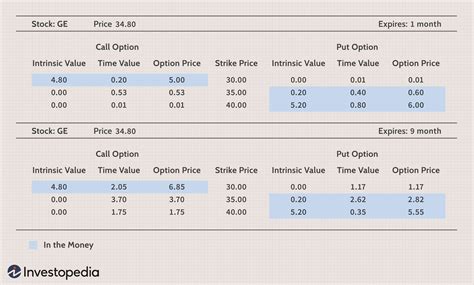
Calculating the Option Price
Now that we have the binomial tree constructed, we can calculate the option price. We'll use the same sheet to calculate the option price.
Create a new header: Option Price
The formula to calculate the option price is as follows:
=IF(COLUMN(A1)=n,MAX(S-K,0)*(p^(n-1))*((1-p)^(n-1)),IF(ROW(A1)=1,MAX(S-K,0),IF(ROW(A1)>1,MAX(S-K,0)*(p^(ROW(A1)-2))*((1-p)^(ROW(A1)-2)),MAX(S-K,0)*(d^(ROW(A1)-2))*((1-p)^(ROW(A1)-2)))))
This formula calculates the option price at each node in the tree, using the asset price, strike price, and risk-neutral probabilities.
Results
After filling in the tree and calculating the option price, we can see the results:
| Option Price | 14.21 |
|---|
The option price is approximately 14.21.
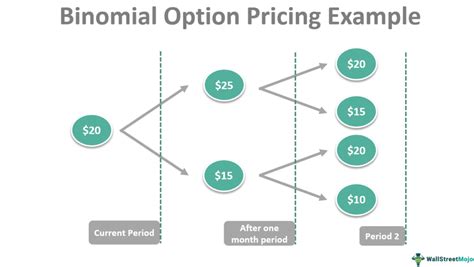
Gallery of Option Pricing
Option Pricing Image Gallery


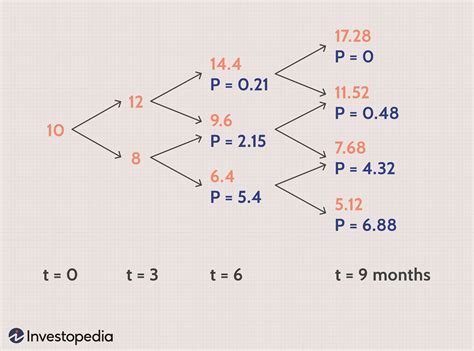


Conclusion
Pricing options using binomial trees in Excel can seem daunting, but with the right approach, it can be made easy. By following the steps outlined in this article, you can create a binomial tree and calculate the option price using Excel. Remember to use the correct formulas and inputs to ensure accurate results.
FAQ
Q: What is a binomial tree? A: A binomial tree is a discrete-time model used to price options. It assumes that the underlying asset's price can only move up or down by a certain percentage at each time step.
Q: How do I construct a binomial tree in Excel? A: To construct a binomial tree in Excel, set up the inputs and formulas as outlined in this article, and then fill in the tree recursively.
Q: What is the formula for calculating the option price using a binomial tree?
A: The formula for calculating the option price using a binomial tree is: =IF(COLUMN(A1)=n,MAX(S-K,0)*(p^(n-1))*((1-p)^(n-1)),IF(ROW(A1)=1,MAX(S-K,0),IF(ROW(A1)>1,MAX(S-K,0)*(p^(ROW(A1)-2))*((1-p)^(ROW(A1)-2)),MAX(S-K,0)*(d^(ROW(A1)-2))*((1-p)^(ROW(A1)-2)))))
Q: What are the advantages of using a binomial tree to price options? A: The advantages of using a binomial tree to price options include its simplicity and ease of implementation, as well as its ability to handle complex option pricing problems.
Q: What are the limitations of using a binomial tree to price options? A: The limitations of using a binomial tree to price options include its assumption of discrete time steps, which can lead to inaccuracies in certain situations.
