Calculating the area under a curve is a common task in various fields such as mathematics, physics, engineering, and finance. In Excel, there are several methods to calculate the area under a curve, and in this article, we will explore the most efficient and easy-to-use methods.
Understanding the Concept of Area Under a Curve
The area under a curve represents the accumulation of the quantity represented by the curve. In other words, it measures the total amount of change of the quantity over a specific interval. The area under a curve can be calculated using various methods, including numerical integration and analytical integration.
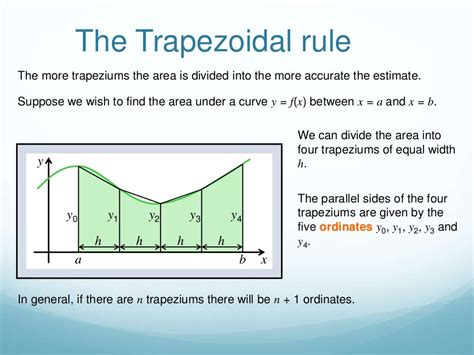
Method 1: Using the Trapezoidal Rule
The trapezoidal rule is a simple and effective method for approximating the area under a curve. This method involves dividing the area under the curve into trapezoids and summing up their areas.
To use the trapezoidal rule in Excel, follow these steps:
- Enter the x-values and corresponding y-values in two columns.
- Create a third column to calculate the width of each trapezoid.
- Calculate the area of each trapezoid using the formula: (y1 + y2) * width / 2.
- Sum up the areas of all trapezoids to get the total area under the curve.
Formula:
Area = Σ ((y1 + y2) * width / 2)
Example:
| x | y | width | Area |
|---|---|---|---|
| 1 | 2 | 0.5 | 2.5 |
| 2 | 4 | 0.5 | 4.5 |
| 3 | 6 | 0.5 | 6.5 |
| ... | ... | ... | ... |
Using Excel Formulas:
=SUM((B2:B10+B3:B11)/2*A3:A10)
where A is the column containing the x-values, B is the column containing the y-values, and the range B2:B10 and B3:B11 corresponds to the y-values and x-values, respectively.
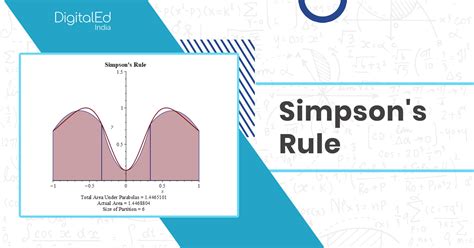
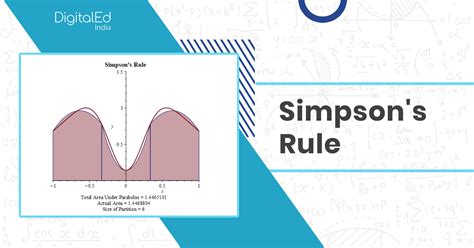
Method 2: Using the Simpson's Rule
Simpson's rule is another numerical integration method that can be used to calculate the area under a curve. This method involves dividing the area under the curve into parabolic segments and summing up their areas.
To use Simpson's rule in Excel, follow these steps:
- Enter the x-values and corresponding y-values in two columns.
- Create a third column to calculate the width of each segment.
- Calculate the area of each segment using the formula: (y1 + 4 * y2 + y3) * width / 6.
- Sum up the areas of all segments to get the total area under the curve.
Formula:
Area = Σ ((y1 + 4 * y2 + y3) * width / 6)
Example:
| x | y | width | Area |
|---|---|---|---|
| 1 | 2 | 0.5 | 3.33 |
| 2 | 4 | 0.5 | 5.33 |
| 3 | 6 | 0.5 | 7.33 |
| ... | ... | ... | ... |
Using Excel Formulas:
=SUM((B2:B10+4*B3:B11+B4:B12)/6*A3:A10)
where A is the column containing the x-values, B is the column containing the y-values, and the range B2:B10, B3:B11, and B4:B12 corresponds to the y-values, x-values, and y-values, respectively.
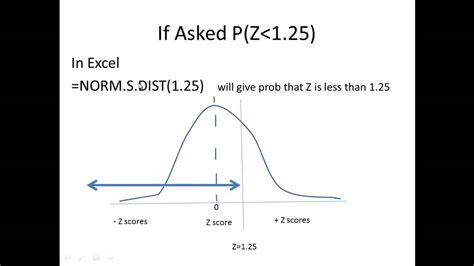
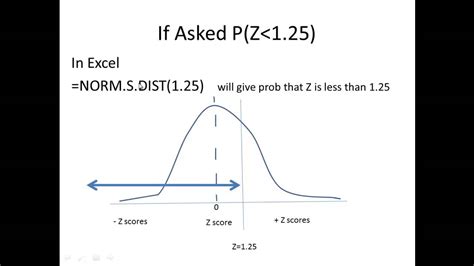
Method 3: Using the Built-in Excel Function
Excel has a built-in function called NORM.S.DIST that can be used to calculate the area under a normal distribution curve.
To use this function, follow these steps:
- Enter the x-value and mean in two cells.
- Enter the standard deviation in another cell.
- Use the formula:
NORM.S.DIST(x, mean, stdev, TRUE).
Example:
| x | mean | stdev | Area |
|---|---|---|---|
| 1 | 0 | 1 | 0.8413 |
Using Excel Formulas:
=NORM.S.DIST(A2, B2, C2, TRUE)
where A is the cell containing the x-value, B is the cell containing the mean, and C is the cell containing the standard deviation.
Gallery of Area Under Curve Images
Area Under Curve Image Gallery




We hope this article has provided you with a comprehensive guide on how to calculate the area under a curve in Excel. Whether you use the trapezoidal rule, Simpson's rule, or the built-in Excel function, you can easily calculate the area under a curve using these methods. Don't hesitate to ask if you have any questions or need further clarification.
