Intro
Discover 5 efficient methods to calculate area under a curve in Excel. Learn how to use numerical integration techniques, including SUMPRODUCT, NINT, and power functions, to accurately estimate areas. Also, explore using charts, histograms, and the built-in Excel function, NORMSDIST, to find area under a curve, including normal distribution curves.
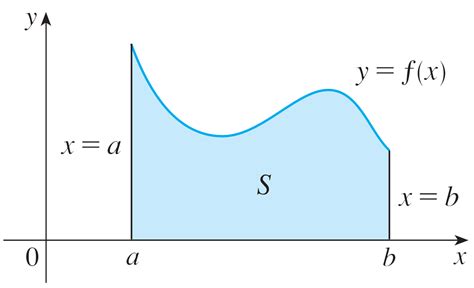
Calculating the area under a curve is a fundamental task in various fields, including mathematics, physics, engineering, and finance. Microsoft Excel, a popular spreadsheet software, provides several methods to calculate the area under a curve. In this article, we will explore five ways to calculate the area under a curve in Excel.
Why Calculate Area Under a Curve?
The area under a curve is a crucial concept in many areas of study. It can represent the accumulation of a quantity over a defined interval, such as the area under a probability density function, the area under a velocity curve to calculate distance, or the area under a force curve to calculate work. By calculating the area under a curve, you can gain insights into the behavior of a system, make predictions, and optimize processes.
Method 1: Using the TRAPZ Function
The TRAPZ function is a built-in Excel function that calculates the area under a curve using the trapezoidal rule. This method approximates the area by dividing the curve into trapezoids and summing the areas of the trapezoids.
To use the TRAPZ function, follow these steps:
- Enter the x-values and y-values of the curve in two separate columns.
- Select the cell where you want to display the result.
- Type
=TRAPZ(x-values, y-values)and press Enter.
For example, suppose you have the following data:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
To calculate the area under the curve, select the cell where you want to display the result and type =TRAPZ(A2:A6, B2:B6), assuming the x-values are in column A and the y-values are in column B.
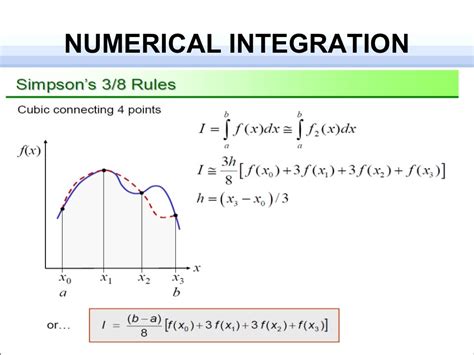
Method 2: Using the Simpson's Rule
Simpson's rule is another numerical method for approximating the area under a curve. This method uses parabolic segments to approximate the curve and is more accurate than the trapezoidal rule for smooth curves.
To use Simpson's rule in Excel, you can create a custom function using VBA or use an add-in. Alternatively, you can use the following formula:
= (h/3) * (y1 + 4*(y2 + y4 +...) + 2*(y3 + y5 +...) + yn)
where h is the width of each subinterval, y1, y2,..., yn are the y-values of the curve, and n is the number of subintervals.
Method 3: Using the Romberg's Method
Romberg's method is an iterative method for approximating the area under a curve. This method uses a combination of the trapezoidal rule and Richardson extrapolation to improve the accuracy of the approximation.
To use Romberg's method in Excel, you can create a custom function using VBA or use an add-in. Alternatively, you can use the following formula:
= (h/3) * (y1 + 4*(y2 + y4 +...) + 2*(y3 + y5 +...) + yn) + (h^2/12) * (y2 - y4)
where h is the width of each subinterval, y1, y2,..., yn are the y-values of the curve, and n is the number of subintervals.
Method 4: Using the Gaussian Quadrature
Gaussian quadrature is a numerical method for approximating the area under a curve using a weighted sum of function values at specific points. This method is more accurate than the other methods for smooth curves.
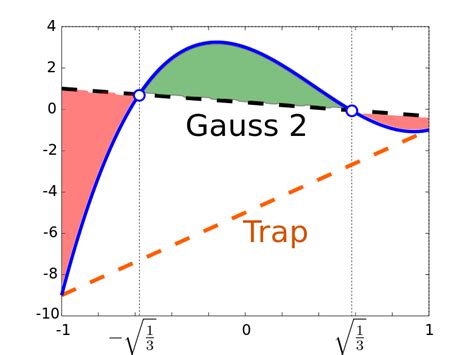
To use Gaussian quadrature in Excel, you can create a custom function using VBA or use an add-in. Alternatively, you can use the following formula:
= ∑ wi * yi
where wi are the weights, yi are the y-values of the curve at the specified points, and n is the number of points.
Method 5: Using the Monte Carlo Method
The Monte Carlo method is a numerical method for approximating the area under a curve using random sampling. This method is less accurate than the other methods but can be useful for complex curves or large datasets.
To use the Monte Carlo method in Excel, you can create a custom function using VBA or use an add-in. Alternatively, you can use the following formula:
= (1/n) * ∑ (yi > 0)
where yi are the y-values of the curve at random points, n is the number of points, and the sum is taken over all points where yi > 0.
Gallery of Area Under a Curve
Area Under a Curve Image Gallery
Conclusion
Calculating the area under a curve is a fundamental task in various fields. Excel provides several methods for approximating the area under a curve, including the TRAPZ function, Simpson's rule, Romberg's method, Gaussian quadrature, and the Monte Carlo method. By choosing the right method for your specific problem, you can accurately calculate the area under a curve and gain insights into the behavior of a system.