5 Trig Functions

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The five main trigonometric functions are sine, cosine, tangent, cotangent, and secant. These functions are used to describe the relationships between the angles and side lengths of triangles, and they have numerous applications in various fields, including physics, engineering, and navigation.

The study of trigonometric functions is essential for anyone who wants to pursue a career in science, technology, engineering, and mathematics (STEM). Understanding the properties and applications of these functions can help individuals solve complex problems and make informed decisions. In this article, we will delve into the world of trigonometric functions, exploring their definitions, properties, and applications.

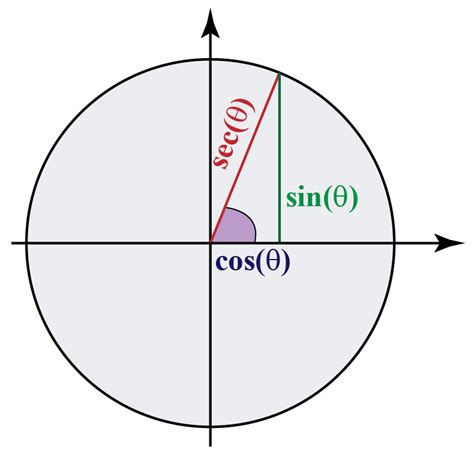
Trigonometric functions are used to describe the relationships between the angles and side lengths of triangles. The most common trigonometric functions are sine, cosine, and tangent, which are defined as the ratios of the lengths of the sides of a right triangle. The sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse, the cosine is defined as the ratio of the length of the adjacent side to the length of the hypotenuse, and the tangent is defined as the ratio of the length of the opposite side to the length of the adjacent side.

Introduction to Trigonometric Functions

The five main trigonometric functions are interrelated and can be used to solve a wide range of problems. Understanding the properties and applications of these functions is essential for anyone who wants to pursue a career in STEM. In this article, we will explore the definitions, properties, and applications of the five main trigonometric functions.

History of Trigonometry

The study of trigonometry dates back to ancient civilizations, with evidence of trigonometric calculations found in the works of ancient Babylonians, Egyptians, and Greeks. The ancient Greeks, in particular, made significant contributions to the development of trigonometry, with mathematicians such as Hipparchus and Euclid making important discoveries about the properties of triangles.

Definitions of Trigonometric Functions

The five main trigonometric functions are defined as follows: * Sine (sin): The ratio of the length of the opposite side to the length of the hypotenuse. * Cosine (cos): The ratio of the length of the adjacent side to the length of the hypotenuse. * Tangent (tan): The ratio of the length of the opposite side to the length of the adjacent side. * Cotangent (cot): The ratio of the length of the adjacent side to the length of the opposite side. * Secant (sec): The ratio of the length of the hypotenuse to the length of the adjacent side.

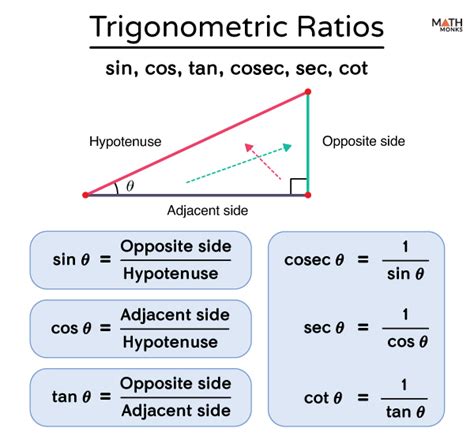
Properties of Trigonometric Functions

Trigonometric functions have several important properties that make them useful for solving problems. Some of the key properties of trigonometric functions include: * Periodicity: Trigonometric functions are periodic, meaning that they repeat themselves at regular intervals. * Symmetry: Trigonometric functions have symmetry properties, meaning that they can be reflected about certain lines or axes. * Identity: Trigonometric functions have identity properties, meaning that they can be simplified or rewritten in different forms.

Applications of Trigonometric Functions

Trigonometric functions have numerous applications in various fields, including physics, engineering, and navigation. Some of the key applications of trigonometric functions include: * Calculating distances and heights: Trigonometric functions can be used to calculate distances and heights in a variety of situations, such as determining the height of a building or the distance to a distant object. * Determining angles: Trigonometric functions can be used to determine angles in a variety of situations, such as calculating the angle of elevation or the angle of depression. * Modeling periodic phenomena: Trigonometric functions can be used to model periodic phenomena, such as the motion of a pendulum or the vibration of a string.

Real-World Examples of Trigonometric Functions

Trigonometric functions are used in a wide range of real-world applications, including: * Navigation: Trigonometric functions are used in navigation systems, such as GPS, to determine the position and direction of a vehicle or aircraft. * Physics: Trigonometric functions are used in physics to describe the motion of objects, including the trajectory of a projectile or the vibration of a string. * Engineering: Trigonometric functions are used in engineering to design and optimize systems, including bridges, buildings, and electronic circuits.

Calculating Trigonometric Functions

Trigonometric functions can be calculated using a variety of methods, including: * Using a calculator: Trigonometric functions can be calculated using a calculator, which can simplify the process and reduce errors. * Using tables: Trigonometric functions can be calculated using tables, which provide pre-calculated values for common angles. * Using formulas: Trigonometric functions can be calculated using formulas, which provide a mathematical expression for the function.

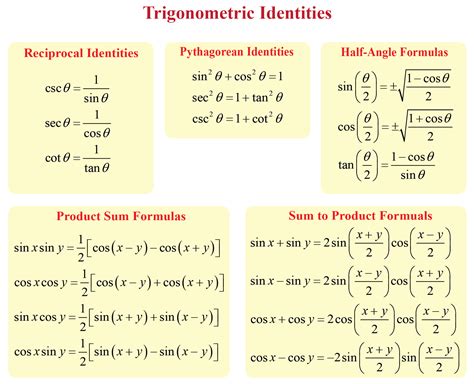
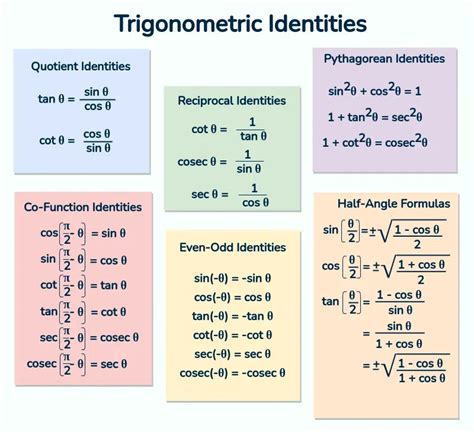
Common Trigonometric Identities

Trigonometric identities are equations that relate different trigonometric functions to each other. Some common trigonometric identities include: * Pythagorean identity: sin^2(x) + cos^2(x) = 1 * Sum and difference identities: sin(a+b) = sin(a)cos(b) + cos(a)sin(b), cos(a+b) = cos(a)cos(b) - sin(a)sin(b) * Double-angle identities: sin(2x) = 2sin(x)cos(x), cos(2x) = 2cos^2(x) - 1

Graphing Trigonometric Functions

Trigonometric functions can be graphed using a variety of methods, including: * Using a graphing calculator: Trigonometric functions can be graphed using a graphing calculator, which can simplify the process and provide a visual representation of the function. * Using software: Trigonometric functions can be graphed using software, such as computer algebra systems or graphing programs. * Using tables: Trigonometric functions can be graphed using tables, which provide pre-calculated values for common angles.

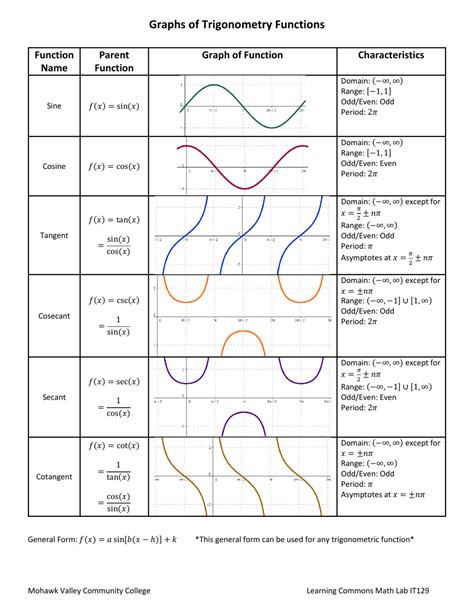
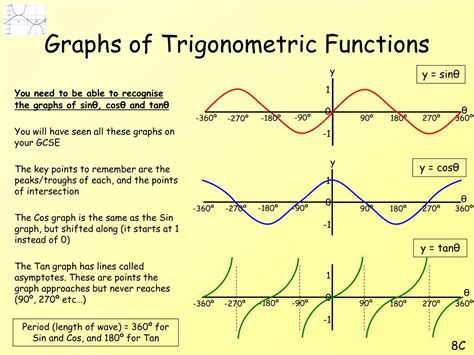
Common Trigonometric Graphs

Some common trigonometric graphs include: * Sine graph: The graph of the sine function is a periodic curve that oscillates between -1 and 1. * Cosine graph: The graph of the cosine function is a periodic curve that oscillates between -1 and 1. * Tangent graph: The graph of the tangent function is a periodic curve that has vertical asymptotes at certain points.

Conclusion and Future Directions

In conclusion, trigonometric functions are an essential part of mathematics and have numerous applications in various fields. Understanding the properties and applications of these functions can help individuals solve complex problems and make informed decisions. As technology continues to advance, the use of trigonometric functions will become even more widespread, and it is essential for individuals to have a strong foundation in these concepts.

Gallery of Trigonometric Functions

Trigonometric Functions Image Gallery

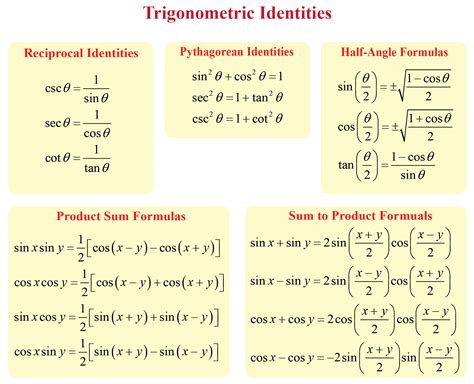
We hope this article has provided you with a comprehensive understanding of trigonometric functions and their applications. If you have any questions or comments, please don't hesitate to reach out. Share this article with your friends and colleagues who may be interested in learning more about trigonometric functions. Additionally, you can take a quiz or practice problems to test your understanding of the concepts presented in this article.