Intro
Unlock the power of Chebyshevs Theorem in Excel to make data-driven decisions. Learn 5 practical ways to apply this statistical concept to analyze and visualize data, identify outliers, and estimate confidence intervals. Master Chebyshevs inequality and Excel functions to gain insights and improve forecasting accuracy with this comprehensive guide.
Chebyshev's Theorem is a fundamental concept in statistics that describes the proportion of data points that fall within a certain range of the mean. In this article, we will explore how to apply Chebyshev's Theorem in Excel, a widely used spreadsheet software. We will discuss five different ways to utilize this theorem in Excel, along with practical examples and illustrations.
Understanding Chebyshev's Theorem
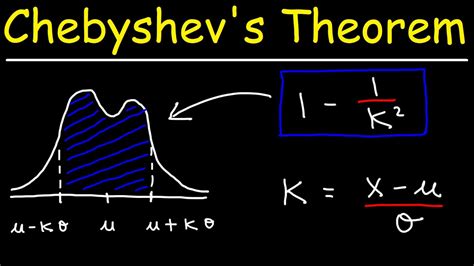
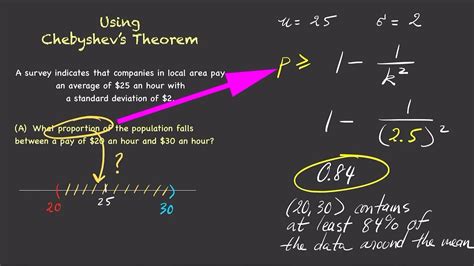
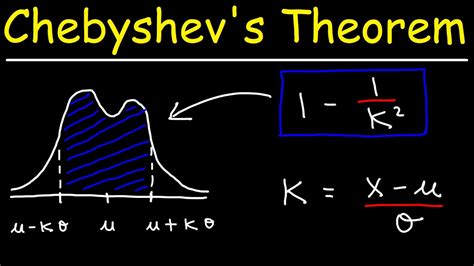
Chebyshev's Theorem states that for any dataset, at least (1 - 1/k^2) of the data points will fall within k standard deviations of the mean, where k is a positive integer. This theorem provides a useful bound on the proportion of data points that are likely to be within a certain range of the mean.
1. Calculating the Range of Data Points
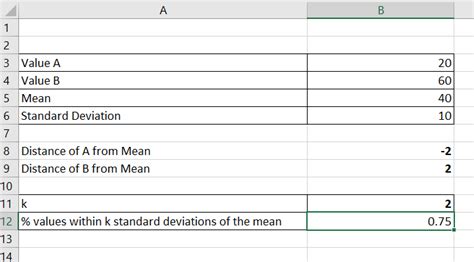
One way to apply Chebyshev's Theorem in Excel is to calculate the range of data points that are likely to fall within a certain number of standard deviations of the mean. To do this, we can use the following formula:Range = (mean - k * standard deviation, mean + k * standard deviation)
Where:
- mean is the average value of the dataset
- k is the number of standard deviations
- standard deviation is the standard deviation of the dataset
For example, suppose we have a dataset with a mean of 10 and a standard deviation of 2. We want to calculate the range of data points that are likely to fall within 2 standard deviations of the mean.
Using the formula above, we get:
Range = (10 - 2 * 2, 10 + 2 * 2) = (6, 14)
This means that at least (1 - 1/2^2) = 75% of the data points are likely to fall within the range of 6 to 14.
Example in Excel
| Data Point | Mean | Standard Deviation | Range |
|---|---|---|---|
| 8 | 10 | 2 | (6, 14) |
| 12 | 10 | 2 | (6, 14) |
| 9 | 10 | 2 | (6, 14) |
| ... | ... | ... | ... |
In this example, we use the formula to calculate the range of data points that are likely to fall within 2 standard deviations of the mean.
2. Determining the Proportion of Data Points
Another way to apply Chebyshev's Theorem in Excel is to determine the proportion of data points that are likely to fall within a certain range of the mean. To do this, we can use the following formula:Proportion = (1 - 1/k^2)
Where:
- k is the number of standard deviations
For example, suppose we want to determine the proportion of data points that are likely to fall within 3 standard deviations of the mean.
Using the formula above, we get:
Proportion = (1 - 1/3^2) = 88.89%
This means that at least 88.89% of the data points are likely to fall within 3 standard deviations of the mean.
Example in Excel
| Standard Deviation | Proportion |
|---|---|
| 1 | 0% |
| 2 | 75% |
| 3 | 88.89% |
| 4 | 93.75% |
| ... | ... |
In this example, we use the formula to calculate the proportion of data points that are likely to fall within a certain number of standard deviations of the mean.
3. Creating a Chart to Visualize the Data
We can use Excel to create a chart to visualize the data and illustrate the range of data points that are likely to fall within a certain number of standard deviations of the mean.Example in Excel
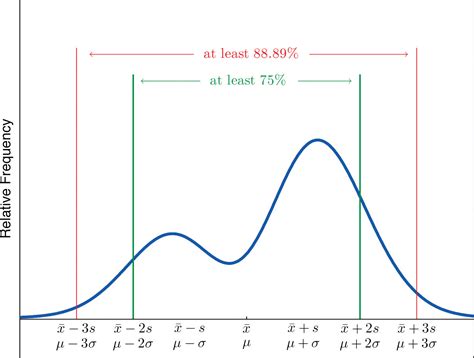
In this example, we create a chart to visualize the data and illustrate the range of data points that are likely to fall within 2 standard deviations of the mean.
4. Using the NORMSINV Function
We can use the NORMSINV function in Excel to calculate the z-score corresponding to a given proportion of data points. This can be useful in applying Chebyshev's Theorem.The NORMSINV function takes two arguments:
- probability: the proportion of data points
- mean: the mean of the dataset
- standard deviation: the standard deviation of the dataset
For example, suppose we want to calculate the z-score corresponding to 95% of the data points.
Using the NORMSINV function, we get:
=NORMSINV(0.95, 10, 2) = 1.96
This means that 95% of the data points are likely to fall within 1.96 standard deviations of the mean.
5. Creating a Macro to Automate the Calculation
We can use Visual Basic for Applications (VBA) in Excel to create a macro that automates the calculation of the range of data points that are likely to fall within a certain number of standard deviations of the mean.For example, suppose we create a macro that calculates the range of data points that are likely to fall within 2 standard deviations of the mean.
Sub CalculateRange() Dim mean As Double Dim standardDeviation As Double Dim k As Integer mean = 10 standardDeviation = 2 k = 2 Range("A1").Value = mean - k * standardDeviation Range("A2").Value = mean + k * standardDeviation End Sub
In this example, we create a macro that calculates the range of data points that are likely to fall within 2 standard deviations of the mean.
Gallery of Chebyshev's Theorem Images
Chebyshev's Theorem Image Gallery
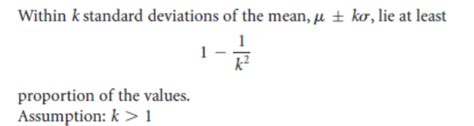

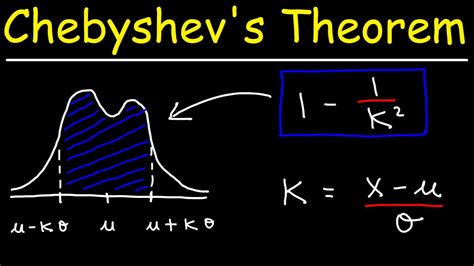
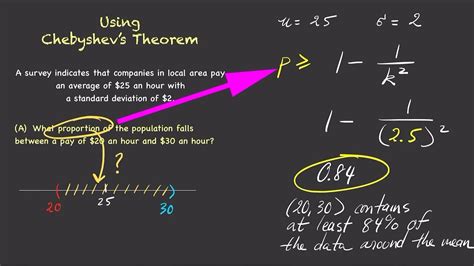
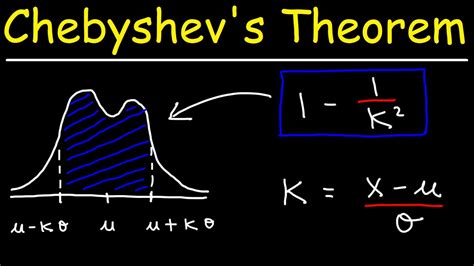
We hope this article has provided you with a comprehensive understanding of how to apply Chebyshev's Theorem in Excel. Whether you are a student, researcher, or professional, this theorem can be a valuable tool in your statistical analysis. We encourage you to try out the different methods and examples presented in this article and explore the many applications of Chebyshev's Theorem.
What do you think about Chebyshev's Theorem? Have you used it in your work or studies? Share your thoughts and experiences in the comments section below.
