Intro
Master the Circle Of Trig Made Easy with simplified explanations, trigonometric functions, and identities, making trigonometry calculations a breeze with related concepts like sine, cosine, and tangent.
The world of trigonometry can be a daunting one, filled with complex formulas and theorems that can leave even the most dedicated students feeling overwhelmed. However, at the heart of trigonometry lies a simple yet powerful concept: the circle of trig. Understanding this fundamental idea is key to unlocking the secrets of trigonometry and making it accessible to everyone. In this article, we will delve into the world of the circle of trig, exploring its importance, its components, and how it can be used to simplify even the most complex trigonometric problems.
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. While it may seem like a niche area of study, trigonometry has numerous real-world applications, from navigation and physics to engineering and computer science. The circle of trig is a crucial tool in trigonometry, as it provides a visual representation of the relationships between different trigonometric functions. By understanding the circle of trig, students can gain a deeper appreciation for the subject and develop the skills they need to succeed in a wide range of fields.
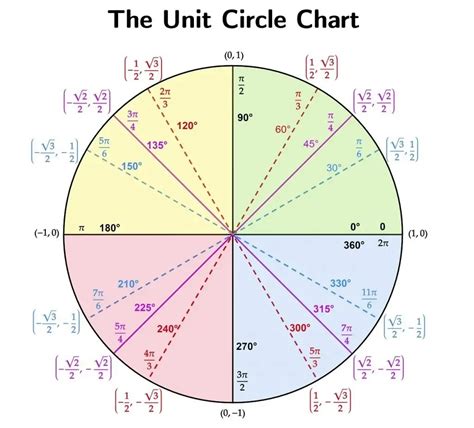
The circle of trig is a circle with a radius of 1, centered at the origin of a coordinate plane. The circle is divided into four quadrants, each representing a different range of angles. The quadrants are labeled I, II, III, and IV, and are defined by the signs of the x and y coordinates. The circle of trig is typically drawn with the positive x-axis to the right and the positive y-axis upwards. This orientation is important, as it allows us to easily identify the relationships between different trigonometric functions.
Introduction to the Circle of Trig
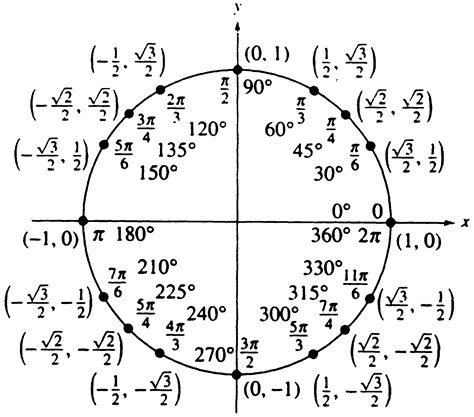
The circle of trig is a powerful tool for visualizing and understanding trigonometric relationships. By using the circle, students can easily identify the values of different trigonometric functions, such as sine, cosine, and tangent. The circle of trig is also useful for identifying the relationships between different trigonometric functions, such as the Pythagorean identity and the sum and difference formulas. These relationships are essential for solving trigonometric problems and are used extensively in a wide range of applications.
Components of the Circle of Trig
The circle of trig is composed of several key components, including the x and y axes, the quadrants, and the unit circle. The x and y axes are the horizontal and vertical lines that intersect at the origin of the coordinate plane. The quadrants are the four regions of the coordinate plane, defined by the signs of the x and y coordinates. The unit circle is the circle with a radius of 1, centered at the origin of the coordinate plane. The unit circle is the foundation of the circle of trig and is used to define the values of different trigonometric functions.Understanding the Unit Circle
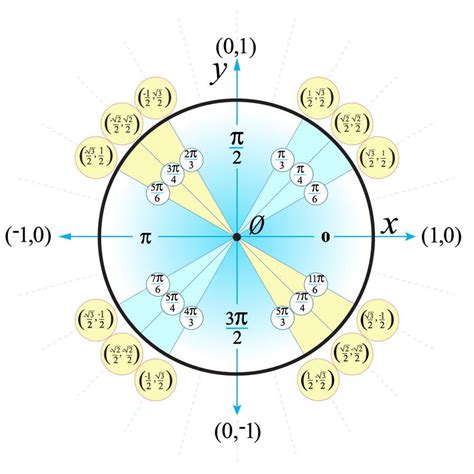
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. The unit circle is used to define the values of different trigonometric functions, such as sine, cosine, and tangent. The unit circle is divided into four quadrants, each representing a different range of angles. The quadrants are labeled I, II, III, and IV, and are defined by the signs of the x and y coordinates. The unit circle is typically drawn with the positive x-axis to the right and the positive y-axis upwards.
Trigonometric Functions
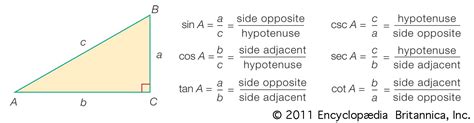
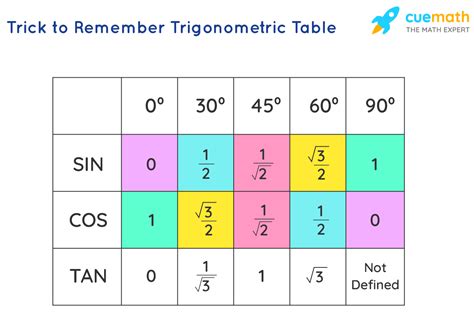
Trigonometric functions are used to describe the relationships between the sides and angles of triangles. The most common trigonometric functions are sine, cosine, and tangent. Sine is defined as the ratio of the length of the side opposite a given angle to the length of the hypotenuse. Cosine is defined as the ratio of the length of the side adjacent to a given angle to the length of the hypotenuse. Tangent is defined as the ratio of the length of the side opposite a given angle to the length of the side adjacent to the angle.Using the Circle of Trig to Simplify Problems

The circle of trig is a powerful tool for simplifying trigonometric problems. By using the circle, students can easily identify the values of different trigonometric functions and identify the relationships between different functions. The circle of trig is also useful for identifying the relationships between different trigonometric functions, such as the Pythagorean identity and the sum and difference formulas. These relationships are essential for solving trigonometric problems and are used extensively in a wide range of applications.
Real-World Applications
Trigonometry has numerous real-world applications, from navigation and physics to engineering and computer science. The circle of trig is a crucial tool in these applications, as it provides a visual representation of the relationships between different trigonometric functions. By understanding the circle of trig, students can gain a deeper appreciation for the subject and develop the skills they need to succeed in a wide range of fields.Common Trigonometric Identities
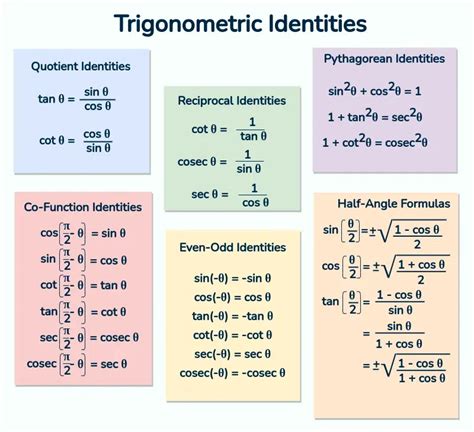
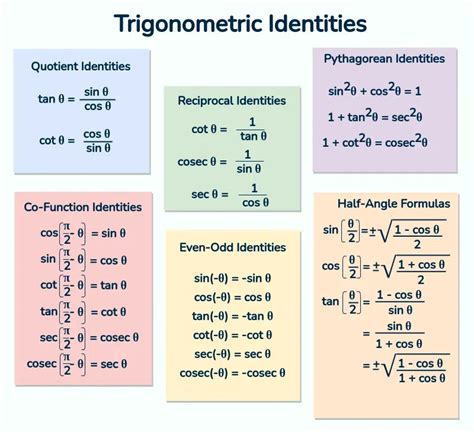
Trigonometric identities are equations that involve trigonometric functions. The most common trigonometric identities are the Pythagorean identity, the sum and difference formulas, and the double angle formulas. The Pythagorean identity states that the sum of the squares of the sine and cosine of an angle is equal to 1. The sum and difference formulas state that the sine and cosine of the sum or difference of two angles can be expressed in terms of the sine and cosine of the individual angles. The double angle formulas state that the sine and cosine of twice an angle can be expressed in terms of the sine and cosine of the angle.
Practice Problems
Practice problems are an essential part of learning trigonometry. By working through practice problems, students can develop their skills and gain a deeper understanding of the subject. Practice problems can be found in a wide range of sources, including textbooks, online resources, and study guides.Solving Trigonometric Equations

Trigonometric equations are equations that involve trigonometric functions. Solving trigonometric equations requires a deep understanding of the subject and the ability to apply trigonometric identities and formulas. The most common method for solving trigonometric equations is to use the unit circle and the trigonometric identities to simplify the equation and solve for the unknown angle.
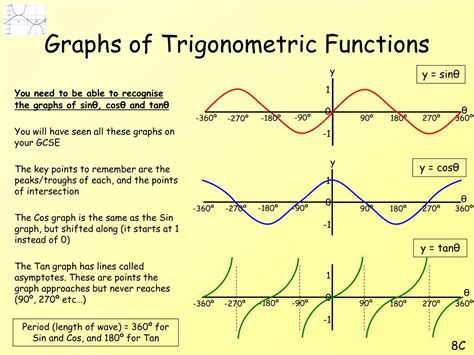
Graphing Trigonometric Functions
Graphing trigonometric functions is an essential part of learning trigonometry. By graphing trigonometric functions, students can visualize the relationships between the sides and angles of triangles and develop a deeper understanding of the subject. The most common trigonometric functions to graph are the sine, cosine, and tangent functions.Trigonometry in Real-World Applications

Trigonometry has numerous real-world applications, from navigation and physics to engineering and computer science. The circle of trig is a crucial tool in these applications, as it provides a visual representation of the relationships between different trigonometric functions. By understanding the circle of trig, students can gain a deeper appreciation for the subject and develop the skills they need to succeed in a wide range of fields.
Conclusion and Next Steps
In conclusion, the circle of trig is a powerful tool for visualizing and understanding trigonometric relationships. By using the circle, students can easily identify the values of different trigonometric functions and identify the relationships between different functions. The circle of trig is also useful for identifying the relationships between different trigonometric functions, such as the Pythagorean identity and the sum and difference formulas. These relationships are essential for solving trigonometric problems and are used extensively in a wide range of applications.Circle of Trig Image Gallery




We hope this article has provided you with a comprehensive understanding of the circle of trig and its importance in trigonometry. Whether you are a student looking to improve your understanding of the subject or a professional seeking to apply trigonometric concepts in your work, the circle of trig is an essential tool to have in your arsenal. We encourage you to share this article with others who may benefit from it and to explore the many resources available online to further your understanding of trigonometry. By working together, we can make trigonometry accessible to everyone and unlock its full potential to solve real-world problems.
