Unlock the secrets of spherical geometry with our in-depth exploration of the cross section of a sphere. Discover the definition, properties, and real-world applications of great circles, small circles, and other 2D shapes that emerge when a sphere is sliced. Dive into the fascinating world of spherical cross sections.
A sphere is a three-dimensional geometric shape that is perfectly symmetrical about its center. It is a closed surface, meaning that it has no beginning or end, and every point on the surface is equidistant from the center. The sphere is a fundamental shape in mathematics, physics, and engineering, and its properties have been studied for centuries.
One of the key features of a sphere is its cross-section. A cross-section is a two-dimensional slice of a three-dimensional object, obtained by intersecting the object with a plane. In the case of a sphere, the cross-section is a circle. Yes, you read that right – a circle!
The circle is a two-dimensional shape that is perfectly symmetrical about its center. It is a closed curve, meaning that it has no beginning or end, and every point on the curve is equidistant from the center. The circle is a fundamental shape in mathematics, and its properties have been studied for centuries.
So, why is the cross-section of a sphere a circle? To understand this, let's consider how a sphere is constructed. Imagine a set of points in three-dimensional space, all equidistant from a central point. As we move these points around the central point, we create a surface that is curved and continuous. This surface is the sphere.
Now, imagine a plane intersecting the sphere. The plane will cut through the sphere, creating a two-dimensional slice. Because the sphere is symmetrical about its center, the cross-section will also be symmetrical. In fact, the cross-section will be a circle, with the center of the circle corresponding to the center of the sphere.

The circle is a fundamental shape in mathematics, and its properties have been studied for centuries. The circle has many interesting properties, including:
- Circumference: The distance around the circle is called the circumference. The circumference of a circle is directly proportional to its radius.
- Area: The area of a circle is the amount of space inside the circle. The area of a circle is directly proportional to the square of its radius.
- Pi: Pi (π) is a mathematical constant that represents the ratio of a circle's circumference to its diameter. Pi is approximately equal to 3.14.
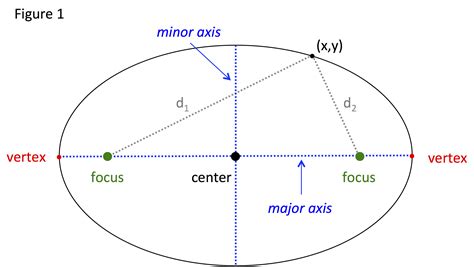
The cross-section of a sphere is not always a circle, however. If the plane intersects the sphere at an angle, the cross-section will be an ellipse. An ellipse is a closed curve that is symmetrical about two axes. The ellipse has many interesting properties, including:
- Major axis: The major axis is the longest diameter of the ellipse.
- Minor axis: The minor axis is the shortest diameter of the ellipse.
- Eccentricity: The eccentricity of an ellipse is a measure of how elliptical it is. An ellipse with an eccentricity of 0 is a circle.
The cross-section of a sphere is a fundamental concept in mathematics and physics. It has many practical applications, including:
- Architecture: The cross-section of a sphere is used in architecture to design buildings and bridges.
- Engineering: The cross-section of a sphere is used in engineering to design structures and mechanisms.
- Physics: The cross-section of a sphere is used in physics to study the properties of materials and objects.
In conclusion, the cross-section of a sphere is a circle or an ellipse, depending on the angle of intersection. The circle and ellipse are fundamental shapes in mathematics, with many interesting properties and practical applications.
Properties of a Sphere
A sphere is a three-dimensional geometric shape that is perfectly symmetrical about its center. It is a closed surface, meaning that it has no beginning or end, and every point on the surface is equidistant from the center. The sphere has many interesting properties, including:
- Center: The center of a sphere is the point that is equidistant from every point on the surface.
- Radius: The radius of a sphere is the distance from the center to any point on the surface.
- Diameter: The diameter of a sphere is the distance from one point on the surface to another point on the surface, passing through the center.
- Circumference: The circumference of a sphere is the distance around the sphere, measured along a great circle.
- Surface area: The surface area of a sphere is the amount of space on the surface of the sphere.
- Volume: The volume of a sphere is the amount of space inside the sphere.
The sphere has many practical applications, including:
- Architecture: The sphere is used in architecture to design buildings and bridges.
- Engineering: The sphere is used in engineering to design structures and mechanisms.
- Physics: The sphere is used in physics to study the properties of materials and objects.
Applications of a Sphere
The sphere has many practical applications in various fields, including:
- Architecture: The sphere is used in architecture to design buildings and bridges. The sphere is used to create curved surfaces that are strong and efficient.
- Engineering: The sphere is used in engineering to design structures and mechanisms. The sphere is used to create curved surfaces that are strong and efficient.
- Physics: The sphere is used in physics to study the properties of materials and objects. The sphere is used to create models of atoms and molecules.
In conclusion, the sphere is a fundamental shape in mathematics, with many interesting properties and practical applications. The sphere is used in various fields, including architecture, engineering, and physics.
Real-World Examples of a Sphere
The sphere is a common shape in the real world, appearing in many natural and man-made objects. Here are some examples:
- Planets: The planets in our solar system are approximately spherical in shape.
- Balls: Balls are spherical objects that are used in sports and games.
- Globes: Globes are spherical models of the Earth or other celestial bodies.
- Bubbles: Bubbles are spherical objects that are created by blowing air into a liquid.

In conclusion, the sphere is a common shape in the real world, appearing in many natural and man-made objects.
Sphere Image Gallery









We hope this article has provided you with a comprehensive understanding of the sphere and its properties. Do you have any questions or comments about the sphere? Please share them with us in the comments section below.
