One-To-One: Meaning, Importance, And Real-Life Applications

In today's fast-paced world, understanding the concept of one-to-one relationships is crucial in various aspects of life, including mathematics, science, and even personal relationships. A one-to-one relationship, also known as a bijective relationship, is a fundamental concept in mathematics that has far-reaching implications in different fields. In this article, we will delve into the meaning, importance, and real-life applications of one-to-one relationships.

What is a One-to-One Relationship?

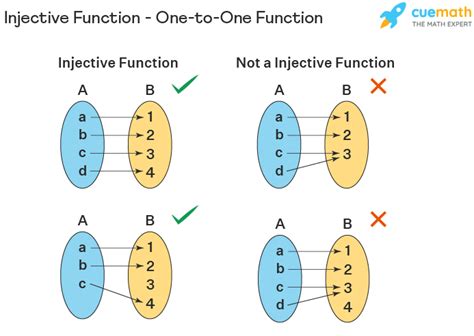
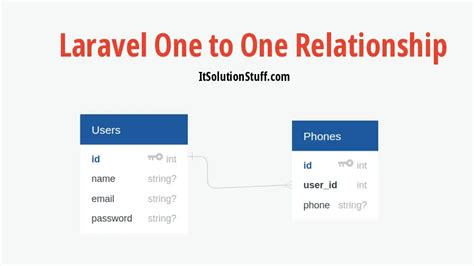
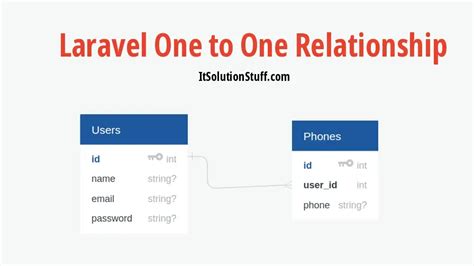
A one-to-one relationship is a type of relationship where each element of one set is paired with exactly one element of another set. In other words, each element in the first set has a unique counterpart in the second set, and vice versa. This type of relationship is also known as a bijective function, where each element in the domain (input) is mapped to exactly one element in the range (output).

Example of a One-to-One Relationship

Consider a simple example of a one-to-one relationship between two sets of numbers. Let's say we have Set A = {1, 2, 3} and Set B = {a, b, c}. A one-to-one relationship between these two sets would mean that each number in Set A is paired with exactly one letter in Set B, and vice versa. For instance:

1 is paired with a
2 is paired with b
3 is paired with c

In this example, each element in Set A has a unique counterpart in Set B, and vice versa.

Importance of One-to-One Relationships

One-to-one relationships play a vital role in various mathematical concepts, including algebra, geometry, and calculus. These relationships help us understand how different variables are related to each other and how they can be used to solve complex problems.

Real-Life Applications of One-to-One Relationships

One-to-one relationships have numerous real-life applications in various fields, including:

Computer Science: One-to-one relationships are used in computer programming to establish unique mappings between variables and values.
Data Analysis: One-to-one relationships are used in data analysis to identify unique patterns and correlations between different variables.
Biology: One-to-one relationships are used in biology to understand the relationships between different species and their habitats.
Economics: One-to-one relationships are used in economics to understand the relationships between different economic variables, such as supply and demand.

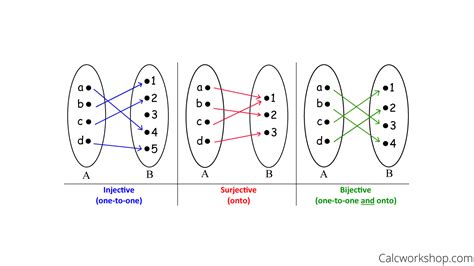
Types of One-to-One Relationships

There are several types of one-to-one relationships, including:

Injective Relationships: A relationship where each element in the domain is mapped to exactly one element in the range.
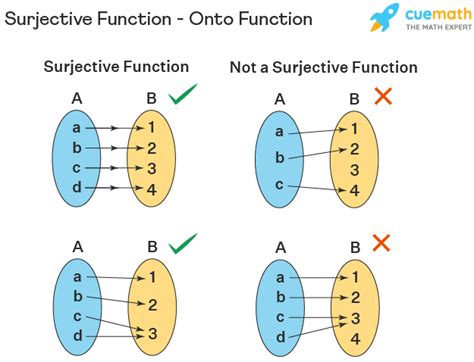
Surjective Relationships: A relationship where each element in the range is mapped to at least one element in the domain.
Bijective Relationships: A relationship where each element in the domain is mapped to exactly one element in the range, and vice versa.

Real-World Examples of One-to-One Relationships

Here are some real-world examples of one-to-one relationships:

Marriage: A one-to-one relationship between two people, where each person is paired with exactly one spouse.
Parent-Child Relationship: A one-to-one relationship between a parent and a child, where each parent is paired with exactly one child.
Student-Teacher Relationship: A one-to-one relationship between a student and a teacher, where each student is paired with exactly one teacher.

Conclusion

In conclusion, one-to-one relationships are a fundamental concept in mathematics that has far-reaching implications in different fields. Understanding the concept of one-to-one relationships is crucial in various aspects of life, including computer science, data analysis, biology, and economics. By recognizing the importance and applications of one-to-one relationships, we can better understand how different variables are related to each other and how they can be used to solve complex problems.

We hope this article has helped you understand the concept of one-to-one relationships and their importance in different fields. If you have any questions or comments, please feel free to share them with us.