Intro
Unlock the power of calculus with the derivative of 9x. Learn the simple calculation and understand the concept of derivatives, functions, and limits. Discover how to apply the power rule and exponential functions to find the derivative of 9x. Improve your math skills with this step-by-step guide to calculus and mathematical functions.
Derivatives are a fundamental concept in calculus, and they have numerous applications in various fields such as physics, engineering, and economics. In this article, we will explore the derivative of 9x, a simple yet important function. We will delve into the concept of derivatives, their importance, and provide a step-by-step guide on how to calculate the derivative of 9x.
What is a Derivative?

A derivative measures how a function changes as its input changes. It represents the rate of change of the function with respect to its variable. Geometrically, the derivative of a function at a point represents the slope of the tangent line to the graph of the function at that point.
Why are Derivatives Important?
Derivatives have numerous applications in various fields, including:
- Optimization: Derivatives are used to optimize functions, which is crucial in fields such as economics, engineering, and physics.
- Physics and Engineering: Derivatives are used to model the motion of objects, forces, and energies.
- Economics: Derivatives are used to analyze the behavior of economic systems, including the behavior of markets and the impact of policy changes.
Calculating the Derivative of 9x

The derivative of 9x can be calculated using the power rule of differentiation, which states that if f(x) = x^n, then f'(x) = nx^(n-1). In this case, n = 1, and f(x) = 9x.
Using the power rule, we can calculate the derivative of 9x as follows:
f'(x) = d(9x)/dx = 9d(x)/dx = 9(1) = 9
Therefore, the derivative of 9x is 9.
Step-by-Step Guide
Here is a step-by-step guide to calculating the derivative of 9x:
- Start with the function f(x) = 9x.
- Apply the power rule of differentiation, which states that if f(x) = x^n, then f'(x) = nx^(n-1).
- In this case, n = 1, and f(x) = 9x.
- Calculate the derivative using the power rule: f'(x) = 9d(x)/dx.
- Simplify the expression: f'(x) = 9(1) = 9.
Examples and Applications

The derivative of 9x has numerous applications in various fields, including physics, engineering, and economics. Here are a few examples:
- Motion along a straight line: The derivative of 9x can be used to model the motion of an object along a straight line, where the object's position is given by the function f(x) = 9x.
- Electric circuits: The derivative of 9x can be used to analyze the behavior of electric circuits, where the voltage and current are related by the function f(x) = 9x.
- Economic models: The derivative of 9x can be used to analyze the behavior of economic systems, including the behavior of markets and the impact of policy changes.
Gallery of Derivative of 9x





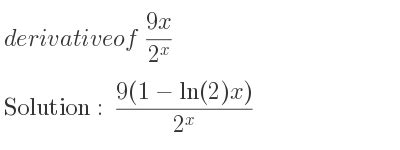


We hope this article has provided you with a clear understanding of the derivative of 9x and its applications. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and feedback in the comments section below!
