Intro
Master the art of calculating 3x3 matrix determinants with our in-depth guide. Discover five distinct methods, including expansion by minors, cofactor expansion, and using the rule of Sarrus. Learn how to apply these techniques to solve systems of linear equations, find eigenvalues, and perform linear transformations with ease and accuracy.
Calculating the determinant of a 3x3 matrix is a fundamental concept in linear algebra and is used in various applications, such as solving systems of linear equations, finding the inverse of a matrix, and determining the area of a parallelogram. In this article, we will explore five different methods to calculate the determinant of a 3x3 matrix.
Understanding the 3x3 Matrix Determinant
The determinant of a 3x3 matrix is a scalar value that can be used to determine the solvability of a system of linear equations. It is also used to find the inverse of a matrix and to determine the area of a parallelogram.
Method 1: Expansion by Minors
One of the most common methods to calculate the determinant of a 3x3 matrix is by expansion by minors. This method involves expanding the determinant along a row or column and calculating the minors of each element.

To calculate the determinant using expansion by minors, we can use the following formula:
det(A) = a(ei − fh) − b(di − fg) + c(dh − eg)
where a, b, c, d, e, f, g, h, and i are the elements of the 3x3 matrix.
Method 2: Rule of Sarrus
The rule of Sarrus is another method to calculate the determinant of a 3x3 matrix. This method involves multiplying the elements of the first row by the corresponding elements of the second and third rows and then subtracting the products of the elements of the second and third rows.

To calculate the determinant using the rule of Sarrus, we can use the following formula:
det(A) = aei + bfg + cdh − ceg − bdi − afh
Method 3: Laplace Expansion
The Laplace expansion is a more general method to calculate the determinant of a matrix. This method involves expanding the determinant along a row or column and calculating the minors of each element.

To calculate the determinant using the Laplace expansion, we can use the following formula:
det(A) = a(ei − fh) − b(di − fg) + c(dh − eg)
Method 4: Cofactor Expansion
The cofactor expansion is a method to calculate the determinant of a matrix by expanding along a row or column and calculating the cofactors of each element.
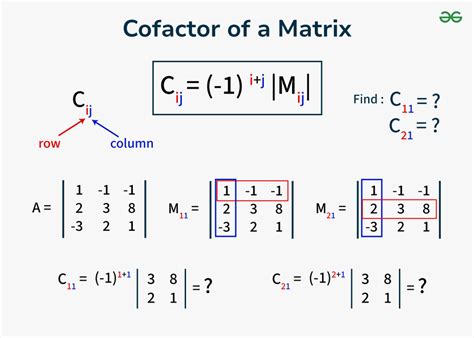
To calculate the determinant using the cofactor expansion, we can use the following formula:
det(A) = a(C11) + b(C12) + c(C13)
where C11, C12, and C13 are the cofactors of the elements a, b, and c, respectively.
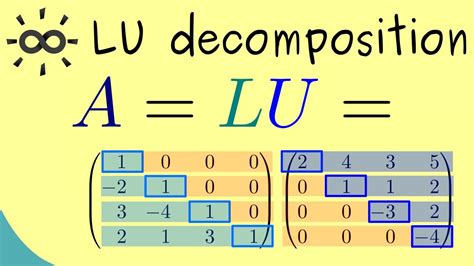
Method 5: LU Decomposition
The LU decomposition is a method to calculate the determinant of a matrix by decomposing it into lower and upper triangular matrices.
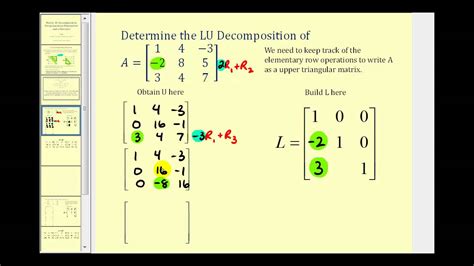
To calculate the determinant using the LU decomposition, we can use the following formula:
det(A) = det(L)det(U)
where L and U are the lower and upper triangular matrices, respectively.
Gallery of 3x3 Matrix Determinant Methods
3x3 Matrix Determinant Methods Gallery


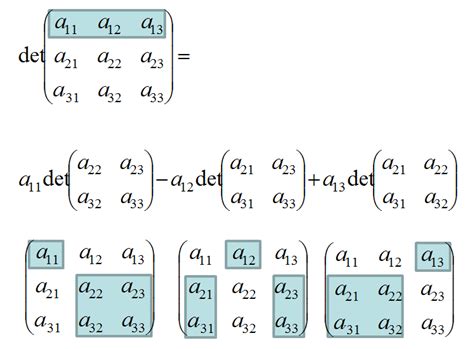






Conclusion
In this article, we have explored five different methods to calculate the determinant of a 3x3 matrix, including expansion by minors, rule of Sarrus, Laplace expansion, cofactor expansion, and LU decomposition. Each method has its own advantages and disadvantages, and the choice of method depends on the specific application and the size of the matrix. We hope that this article has provided a comprehensive understanding of the different methods to calculate the determinant of a 3x3 matrix.
We encourage you to share your thoughts and comments on this article. Have you used any of these methods to calculate the determinant of a 3x3 matrix? Which method do you think is the most efficient? Share your experiences and insights with us!
