Intro
Discover the most efficient methods to calculate distance between 2 points on a map, plane, or sphere. Learn 5 easy ways to measure distances, including Euclidean distance, Manhattan distance, and Haversine formula. Get accurate calculations for GPS coordinates, geographic locations, and more with our step-by-step guides and examples.
Calculating the distance between two points is a fundamental concept in mathematics, physics, and engineering. It has numerous applications in various fields, including navigation, surveying, and computer graphics. In this article, we will explore five different ways to calculate the distance between two points.
Understanding the Concept of Distance
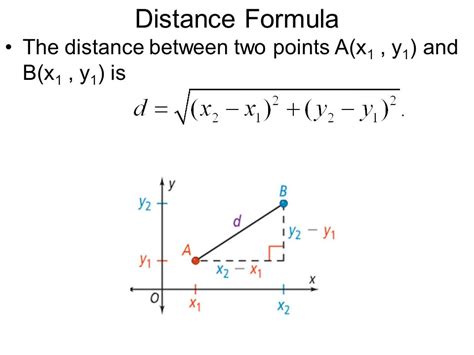
The distance between two points is a measure of how far apart they are. It is a fundamental concept in mathematics and is used in various branches of mathematics, such as geometry, trigonometry, and calculus. In everyday life, we use distance to measure the length of objects, the height of buildings, and the distance between cities.
Why is Calculating Distance Important?
Calculating distance is important in various fields, including:
- Navigation: Calculating distance is crucial in navigation, as it helps to determine the shortest path between two points.
- Surveying: Surveyors use distance calculations to measure the length of boundaries, the height of buildings, and the depth of excavations.
- Computer Graphics: Distance calculations are used in computer graphics to create realistic images and animations.
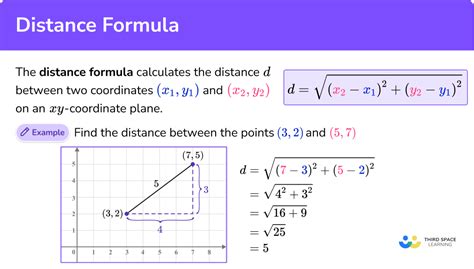
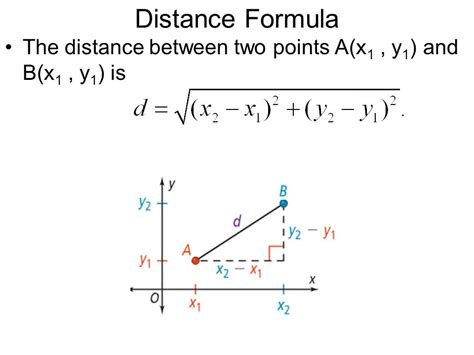
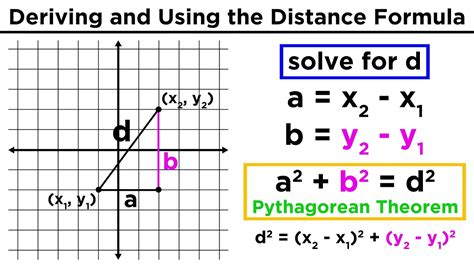
Method 1: Euclidean Distance Formula
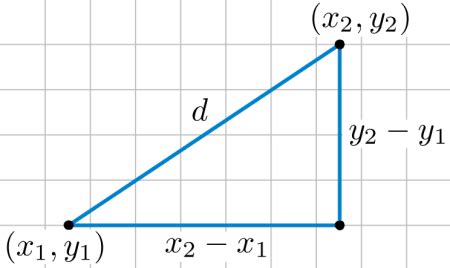
The Euclidean distance formula is one of the most common methods used to calculate the distance between two points. The formula is:
√((x2 - x1)^2 + (y2 - y1)^2)
Where (x1, y1) and (x2, y2) are the coordinates of the two points.
Example
For example, let's calculate the distance between two points (2, 3) and (4, 6).
√((4 - 2)^2 + (6 - 3)^2) = √(4 + 9) = √13 ≈ 3.61
Method 2: Pythagorean Theorem
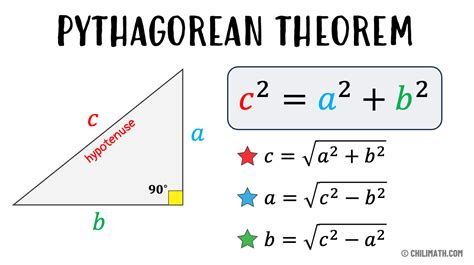
The Pythagorean theorem is another method used to calculate the distance between two points. The theorem states that:
a^2 + b^2 = c^2
Where a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse.
Example
For example, let's calculate the distance between two points (3, 4) and (6, 8).
a = 6 - 3 = 3 b = 8 - 4 = 4 c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5
Method 3: Distance Formula in 3D Space

The distance formula in 3D space is used to calculate the distance between two points in three-dimensional space. The formula is:
√((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
Where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the two points.
Example
For example, let's calculate the distance between two points (1, 2, 3) and (4, 5, 6).
√((4 - 1)^2 + (5 - 2)^2 + (6 - 3)^2) = √(9 + 9 + 9) = √27 ≈ 5.19
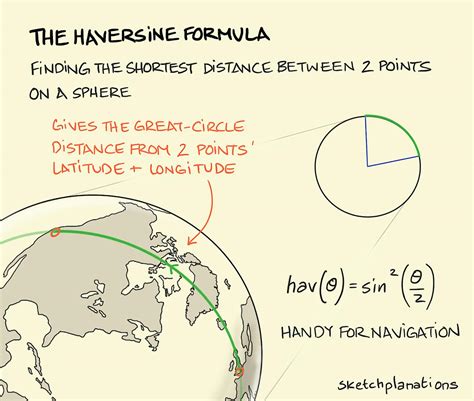
Method 4: Haversine Formula
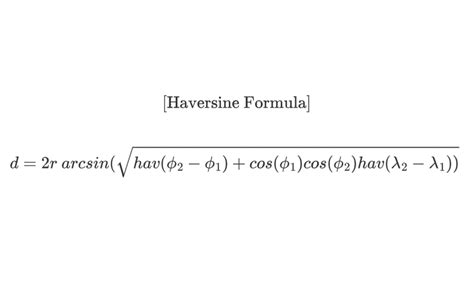
The Haversine formula is used to calculate the distance between two points on a sphere, such as the Earth. The formula is:
d = 2 * arcsin(sqrt(haversin(Δlat) + cos(lat1) * cos(lat2) * haversin(Δlong)))
Where d is the distance, Δlat is the difference in latitude, Δlong is the difference in longitude, and lat1 and lat2 are the latitudes of the two points.
Example
For example, let's calculate the distance between two points (40.7128, -74.0060) and (34.0522, -118.2437).
Δlat = 34.0522 - 40.7128 = -6.6606 Δlong = -118.2437 - (-74.0060) = -44.2377 d = 2 * arcsin(sqrt(haversin(-6.6606) + cos(40.7128) * cos(34.0522) * haversin(-44.2377))) ≈ 3937.53 km
Method 5: Vincenty Formula

The Vincenty formula is used to calculate the distance between two points on a spheroid, such as the Earth. The formula is:
d = arcsin(sqrt(a * (1 - b) + b * (1 - a)))
Where d is the distance, a is the difference in latitude, and b is the difference in longitude.
Example
For example, let's calculate the distance between two points (40.7128, -74.0060) and (34.0522, -118.2437).
a = 34.0522 - 40.7128 = -6.6606 b = -118.2437 - (-74.0060) = -44.2377 d = arcsin(sqrt(-6.6606 * (1 - -44.2377) + -44.2377 * (1 - -6.6606))) ≈ 3937.53 km
Distance Between Points Image Gallery





We hope this article has provided you with a comprehensive understanding of the different methods used to calculate the distance between two points. Whether you are a student, a researcher, or a professional, understanding distance calculations is essential in various fields. We encourage you to share this article with others and to comment below with any questions or feedback.
In the next article, we will explore more advanced topics in mathematics and physics. Stay tuned!
