5 Ways To Master Distance Between Two Points

Calculating the distance between two points is a fundamental concept in mathematics, physics, and engineering. It's a crucial skill to master, as it has numerous applications in various fields, including navigation, architecture, and data analysis. In this article, we'll explore five ways to calculate the distance between two points, from basic to advanced methods.

Understanding the Basics

Before diving into the methods, let's understand the basic concept of distance between two points. In a two-dimensional space, two points are represented by their coordinates (x1, y1) and (x2, y2). The distance between these points is the length of the straight line connecting them. In a three-dimensional space, the concept is similar, but we need to consider the z-coordinate as well.

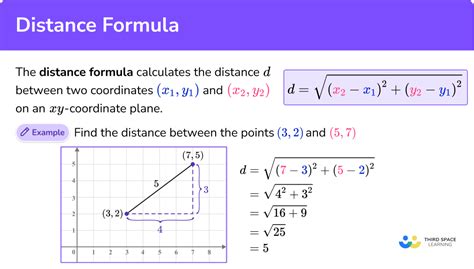
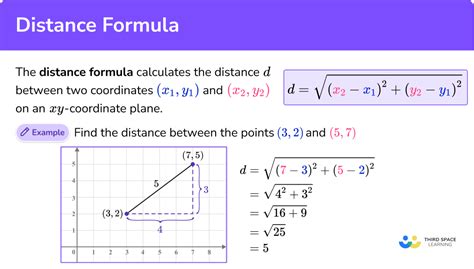
Method 1: Using the Distance Formula

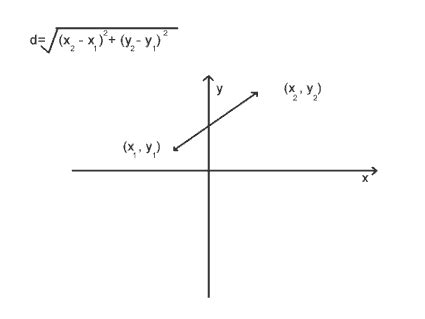
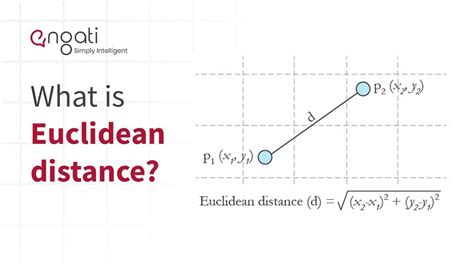
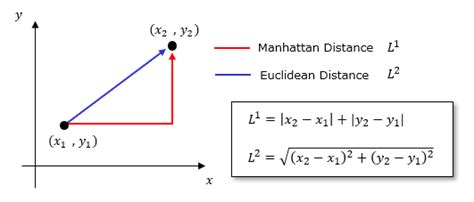
The most straightforward method to calculate the distance between two points is by using the distance formula. This formula is derived from the Pythagorean theorem and is applicable in both two-dimensional and three-dimensional spaces.

For two-dimensional space:

Distance = √((x2 - x1)^2 + (y2 - y1)^2)

For three-dimensional space:

Distance = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)

This formula is simple to apply and provides accurate results.

Method 2: Using Trigonometry

Another method to calculate the distance between two points is by using trigonometry. This method involves calculating the angle between the two points and then using the cosine law to find the distance.

For two-dimensional space:

Distance = √(x1^2 + x2^2 - 2x1x2cos(θ))

For three-dimensional space:

Distance = √(x1^2 + x2^2 + z1^2 + z2^2 - 2x1x2cos(θ) - 2z1z2cos(θ))

This method is useful when the coordinates of the points are not known, but the angle between them is.

Method 3: Using Vectors

Vectors can also be used to calculate the distance between two points. This method involves subtracting the coordinates of one point from the other and then finding the magnitude of the resulting vector.

For two-dimensional space:

Vector = (x2 - x1, y2 - y1) Distance = √(Vector.x^2 + Vector.y^2)

For three-dimensional space:

Vector = (x2 - x1, y2 - y1, z2 - z1) Distance = √(Vector.x^2 + Vector.y^2 + Vector.z^2)

This method is useful when working with vectors and is a fundamental concept in physics and engineering.

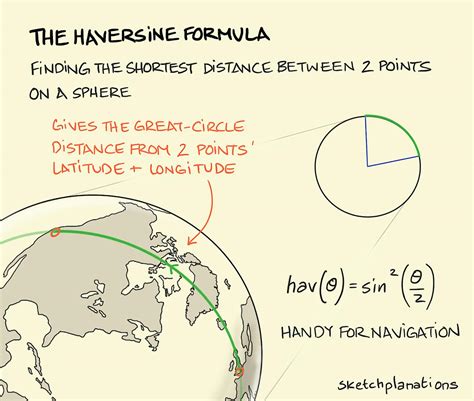
Method 4: Using the Haversine Formula

The Haversine formula is used to calculate the distance between two points on a sphere, such as the Earth. This formula is useful in navigation and geography.

Distance = 2 * arcsin(√(haversin(Δlat) + cos(lat1) * cos(lat2) * haversin(Δlong)))

where Δlat and Δlong are the differences in latitude and longitude between the two points.

This method is accurate for small distances, but less accurate for larger distances.

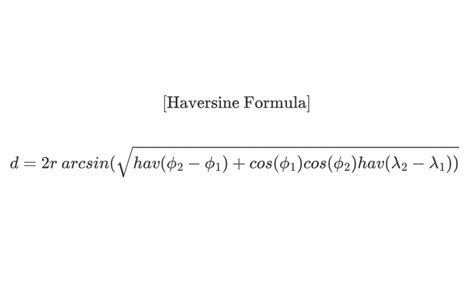
Method 5: Using Machine Learning

Machine learning algorithms can also be used to estimate the distance between two points. This method involves training a model on a dataset of known distances and then using the model to predict the distance between two new points.

There are several machine learning algorithms that can be used for this task, including neural networks, decision trees, and random forests.

This method is useful when the coordinates of the points are not known, but the distance between them can be estimated based on other factors.

Gallery of Distance Calculation Methods

Distance Calculation Methods

Conclusion

Calculating the distance between two points is a fundamental concept in mathematics and physics. There are several methods to calculate distance, ranging from simple formulas to advanced machine learning algorithms. Each method has its strengths and weaknesses, and the choice of method depends on the specific application and the accuracy required.

We hope this article has provided you with a comprehensive understanding of the different methods to calculate distance between two points. Whether you're a student, researcher, or professional, mastering these methods will help you solve complex problems in your field.

Feel free to share your thoughts and questions in the comments section below.