5 Ways To Fix Divide By Zero Error Encountered

Divide by zero errors can be a frustrating issue to encounter, especially when working with mathematical operations or programming. This type of error occurs when a program or formula attempts to divide a number by zero, which is undefined in mathematics. In this article, we will explore five ways to fix divide by zero errors and provide practical examples to help you overcome this issue.

Understanding Divide by Zero Errors

Before we dive into the solutions, it's essential to understand why divide by zero errors occur. In mathematics, division is defined as the inverse operation of multiplication. However, when you divide a number by zero, the result is undefined because zero does not have a multiplicative inverse.

In programming, divide by zero errors can occur due to various reasons such as:

• Insufficient input validation
• Incorrect data types
• Inadequate error handling
• Poor algorithm design

1. Input Validation

One of the simplest ways to fix divide by zero errors is to validate user input. Before performing any division operation, check if the divisor is zero. If it is, display an error message or handle the exception accordingly.

For example, in Python:

def divide_numbers(dividend, divisor):
    if divisor == 0:
        return "Error: Division by zero is not allowed"
    else:
        return dividend / divisor

Benefits of Input Validation

• Prevents divide by zero errors
• Improves user experience by providing meaningful error messages
• Enhances code robustness and reliability

2. Try-Except Blocks

Another approach to handle divide by zero errors is to use try-except blocks. This method allows you to catch the exception and provide a default value or handle the error accordingly.

For example, in Java:

public class DivisionExample {
    public static void main(String[] args) {
        try {
            int dividend = 10;
            int divisor = 0;
            int result = divide(dividend, divisor);
            System.out.println("Result: " + result);
        } catch (ArithmeticException e) {
            System.out.println("Error: " + e.getMessage());
        }
    }

    public static int divide(int dividend, int divisor) {
        return dividend / divisor;
    }
}

Benefits of Try-Except Blocks

• Provides a structured way to handle exceptions
• Allows for custom error handling and default values
• Enhances code readability and maintainability

3. Safe Division Functions

Some programming languages and libraries provide safe division functions that return a default value or handle the exception automatically. These functions can be used to avoid divide by zero errors.

For example, in MATLAB:

function result = safe_divide(dividend, divisor)
    if divisor == 0
        result = NaN; % Return Not a Number (NaN)
    else
        result = dividend / divisor;
    end
end

Benefits of Safe Division Functions

• Provides a convenient way to handle divide by zero errors
• Reduces code complexity and improves readability
• Enhances code reliability and robustness

4. Alternative Mathematical Operations

In some cases, you can avoid divide by zero errors by using alternative mathematical operations. For example, instead of dividing by a variable, you can multiply by its reciprocal.

For example, in Python:

def alternative_division(dividend, divisor):
    if divisor == 0:
        return "Error: Division by zero is not allowed"
    else:
        reciprocal = 1 / divisor
        return dividend * reciprocal

Benefits of Alternative Mathematical Operations

• Provides a creative way to avoid divide by zero errors
• Enhances code flexibility and adaptability
• Improves code maintainability and readability

5. Rounding and Approximations

In some cases, you can use rounding and approximations to avoid divide by zero errors. This approach involves rounding the divisor to a small non-zero value or using an approximation instead of the exact value.

For example, in C++:

#include 

double safe_divide(double dividend, double divisor) {
    if (std::abs(divisor) < 1e-9) {
        divisor = 1e-9; // Round to a small non-zero value
    }
    return dividend / divisor;
}

Benefits of Rounding and Approximations

• Provides a simple way to avoid divide by zero errors
• Enhances code performance and efficiency
• Improves code reliability and robustness

Divide by Zero Error Encountered Image Gallery

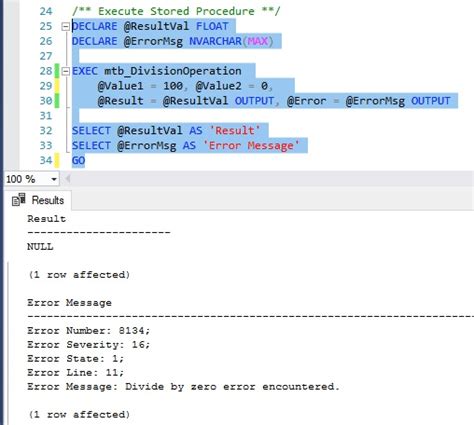
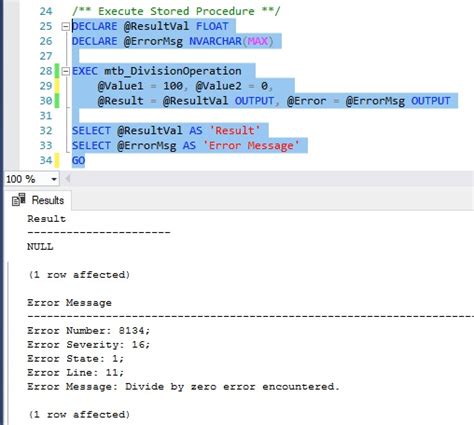
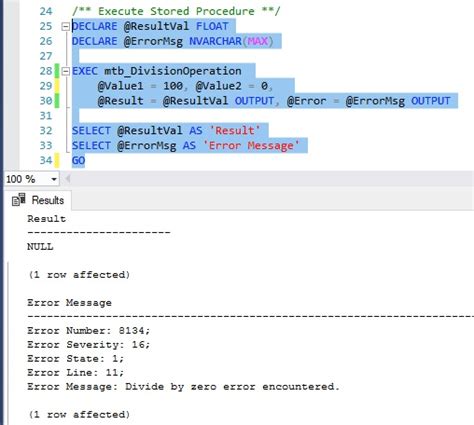
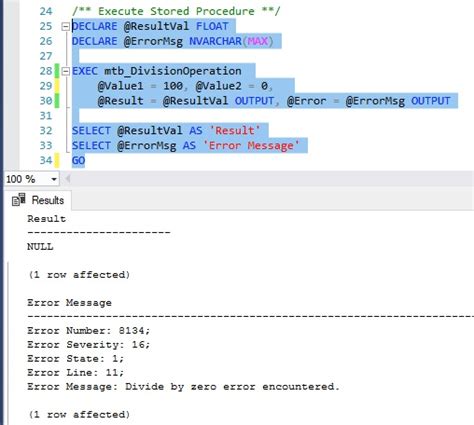
In conclusion, divide by zero errors can be a challenging issue to overcome, but there are several ways to fix them. By using input validation, try-except blocks, safe division functions, alternative mathematical operations, and rounding and approximations, you can avoid divide by zero errors and ensure your code is robust and reliable.