Learn 5 easy multiply methods, including multiplication tables, arrays, and partial products, to improve math skills and master multiplication techniques with simple strategies and practice exercises.
Multiplication is a fundamental concept in mathematics that can be challenging for some individuals, especially when dealing with large numbers. However, with the right techniques and strategies, multiplying numbers can become easier and more efficient. In this article, we will explore five easy multiply methods that can help simplify the multiplication process.
Multiplication is an essential skill that is used in various aspects of life, from basic arithmetic to complex mathematical calculations. Mastering multiplication can help individuals solve problems more quickly and accurately, which is crucial in fields such as science, technology, engineering, and mathematics (STEM). Moreover, developing strong multiplication skills can also improve mental math abilities, making it easier to perform calculations in everyday life.
The importance of multiplication cannot be overstated, and it is essential to develop effective strategies for multiplying numbers. Traditional multiplication methods can be time-consuming and prone to errors, especially when dealing with large numbers. However, by using alternative methods, individuals can simplify the multiplication process and reduce the risk of errors. In the following sections, we will discuss five easy multiply methods that can help make multiplication easier and more efficient.
Introduction to Easy Multiply Methods
These methods are designed to simplify the multiplication process by breaking down numbers into smaller, more manageable parts. By using these strategies, individuals can reduce the risk of errors and perform calculations more quickly. The five easy multiply methods discussed in this article include the lattice method, the Napier's bones method, the grid method, the partial products method, and the mental math method.
The Lattice Method
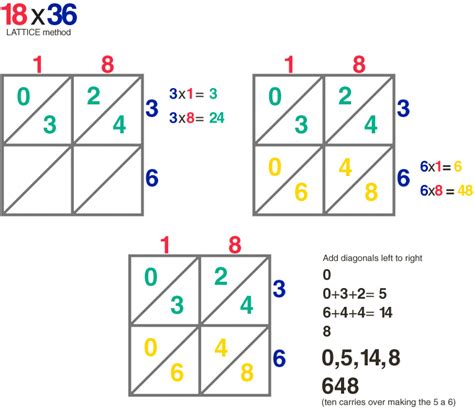
The lattice method is a visual approach to multiplication that involves creating a lattice or grid to represent the multiplication problem. This method is particularly useful for multiplying large numbers, as it helps to break down the calculation into smaller, more manageable parts. To use the lattice method, individuals start by creating a grid with the multiplicand (the number being multiplied) on one axis and the multiplier (the number by which we are multiplying) on the other axis.
Steps for the Lattice Method
The lattice method involves the following steps: * Create a grid with the multiplicand on one axis and the multiplier on the other axis. * Fill in the grid by multiplying each digit of the multiplicand by each digit of the multiplier. * Add up the products to find the final answer.For example, to multiply 43 by 27 using the lattice method, individuals would create a grid with 43 on one axis and 27 on the other axis. They would then fill in the grid by multiplying each digit of 43 by each digit of 27, and finally add up the products to find the final answer.
The Napier's Bones Method
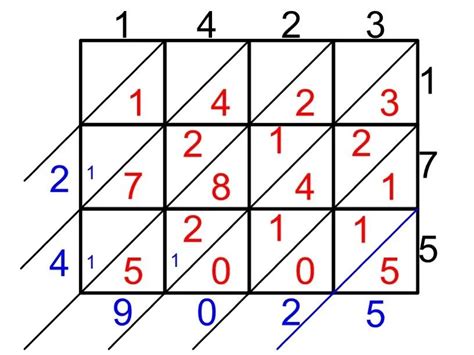
Napier's bones is a manual method of multiplication that uses a set of rods or bones to represent the multiplicand and multiplier. This method was invented by John Napier, a Scottish mathematician, in the 17th century. To use Napier's bones, individuals start by setting up the multiplicand and multiplier on the rods, and then use a series of multiplication tables to find the product.
Steps for Napier's Bones Method
The Napier's bones method involves the following steps: * Set up the multiplicand and multiplier on the rods. * Use the multiplication tables to find the product of each digit of the multiplicand and multiplier. * Add up the products to find the final answer.For example, to multiply 34 by 25 using Napier's bones, individuals would set up the multiplicand (34) and multiplier (25) on the rods, and then use the multiplication tables to find the product of each digit. They would then add up the products to find the final answer.
The Grid Method
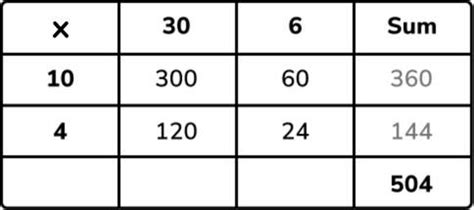
The grid method is a visual approach to multiplication that involves creating a grid to represent the multiplication problem. This method is similar to the lattice method, but it uses a simpler grid structure. To use the grid method, individuals start by creating a grid with the multiplicand on one axis and the multiplier on the other axis.
Steps for the Grid Method
The grid method involves the following steps: * Create a grid with the multiplicand on one axis and the multiplier on the other axis. * Fill in the grid by multiplying each digit of the multiplicand by each digit of the multiplier. * Add up the products to find the final answer.For example, to multiply 56 by 32 using the grid method, individuals would create a grid with 56 on one axis and 32 on the other axis. They would then fill in the grid by multiplying each digit of 56 by each digit of 32, and finally add up the products to find the final answer.
The Partial Products Method

The partial products method is a strategy for multiplying large numbers by breaking them down into smaller parts. This method involves multiplying each digit of the multiplicand by each digit of the multiplier, and then adding up the products to find the final answer.
Steps for the Partial Products Method
The partial products method involves the following steps: * Break down the multiplicand and multiplier into smaller parts. * Multiply each digit of the multiplicand by each digit of the multiplier. * Add up the products to find the final answer.For example, to multiply 67 by 49 using the partial products method, individuals would break down the multiplicand (67) and multiplier (49) into smaller parts. They would then multiply each digit of 67 by each digit of 49, and finally add up the products to find the final answer.
The Mental Math Method

The mental math method is a strategy for multiplying numbers in your head. This method involves using mental calculations to find the product of two numbers. To use the mental math method, individuals start by breaking down the multiplicand and multiplier into smaller parts.
Steps for the Mental Math Method
The mental math method involves the following steps: * Break down the multiplicand and multiplier into smaller parts. * Use mental calculations to find the product of each digit. * Add up the products to find the final answer.For example, to multiply 23 by 17 using the mental math method, individuals would break down the multiplicand (23) and multiplier (17) into smaller parts. They would then use mental calculations to find the product of each digit, and finally add up the products to find the final answer.
Gallery of Multiply Methods
Multiply Methods Image Gallery
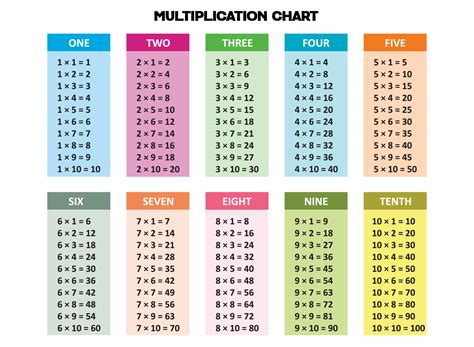

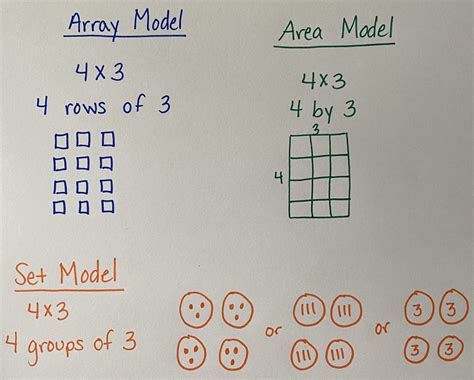
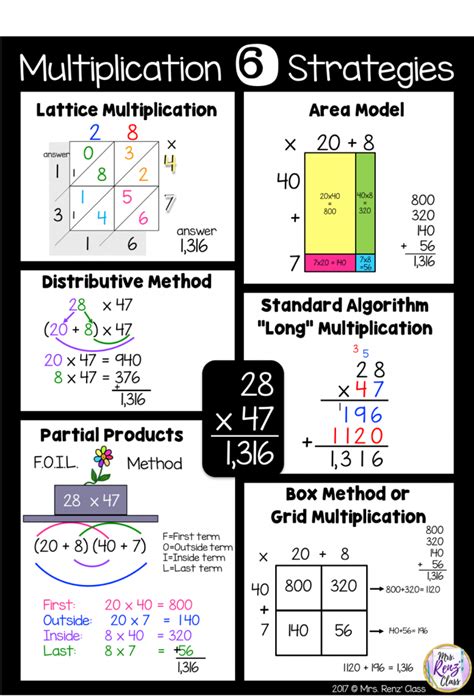





In conclusion, mastering multiplication is an essential skill that can help individuals solve problems more quickly and accurately. By using the five easy multiply methods discussed in this article, individuals can simplify the multiplication process and reduce the risk of errors. Whether you are a student, teacher, or professional, developing strong multiplication skills can help you achieve your goals and succeed in your endeavors. We encourage you to try out these methods and practice regularly to improve your multiplication skills. Share your thoughts and experiences with us in the comments below, and don't forget to share this article with your friends and family who may benefit from these easy multiply methods.
