Eigenvalues And Eigenvectors In Excel Made Easy

In the world of linear algebra, eigenvalues and eigenvectors are two fundamental concepts that can be quite intimidating, especially when it comes to calculating them manually. Fortunately, Microsoft Excel provides an efficient way to compute these values, making it easier to understand and work with them. In this article, we will explore the world of eigenvalues and eigenvectors, and learn how to calculate them using Excel.

What are Eigenvalues and Eigenvectors?

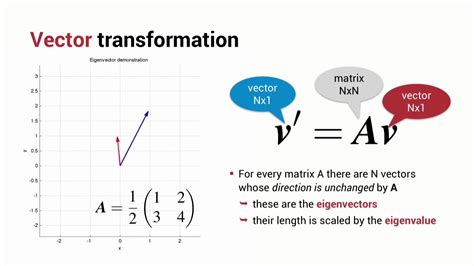
In linear algebra, eigenvalues and eigenvectors are used to describe the behavior of linear transformations. Given a square matrix A, an eigenvector is a non-zero vector v such that when the matrix A is multiplied by v, the result is a scaled version of v. The scalar that multiplies v is called the eigenvalue.

Mathematically, this can be represented as:

Av = λv

where A is the square matrix, v is the eigenvector, and λ is the eigenvalue.

Importance of Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors have numerous applications in various fields, including physics, engineering, computer science, and data analysis. Some of the key uses of eigenvalues and eigenvectors include:

• Stability analysis: Eigenvalues can be used to determine the stability of a system.
• Data compression: Eigenvectors can be used to reduce the dimensionality of high-dimensional data.
• Image processing: Eigenvectors can be used for image compression and reconstruction.
• Machine learning: Eigenvalues and eigenvectors are used in various machine learning algorithms, such as PCA (Principal Component Analysis).

Calculating Eigenvalues and Eigenvectors in Excel

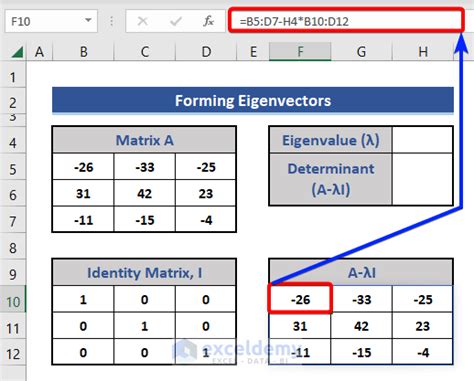
Excel provides a built-in function called the "Eigenvalue" function, which can be used to calculate the eigenvalues and eigenvectors of a square matrix. Here's how to use it:

1. Enter the square matrix A in a range of cells, say A1:E4.
2. Go to the "Formulas" tab in the ribbon and click on "More Functions" in the "Functions Library" group.
3. In the "Function Arguments" dialog box, select the "Eigenvalue" function.
4. In the "Matrix" field, enter the range of cells containing the matrix A.
5. In the "Eigenvalue" field, enter the cell where you want to display the eigenvalue.
6. Click "OK" to calculate the eigenvalue.

To calculate the eigenvector, follow these steps:

1. Enter the square matrix A in a range of cells, say A1:E4.
2. Go to the "Formulas" tab in the ribbon and click on "More Functions" in the "Functions Library" group.
3. In the "Function Arguments" dialog box, select the "Eigenvector" function.
4. In the "Matrix" field, enter the range of cells containing the matrix A.
5. In the "Eigenvector" field, enter the cell where you want to display the eigenvector.
6. Click "OK" to calculate the eigenvector.

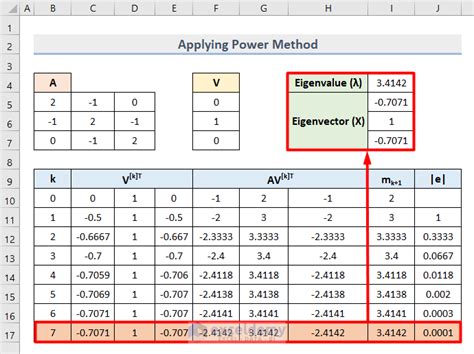
Example: Calculating Eigenvalues and Eigenvectors in Excel

Suppose we have a 3x3 matrix A:

| 2 1 1 | | 1 2 1 | | 1 1 2 |

To calculate the eigenvalues and eigenvectors of this matrix, follow these steps:

1. Enter the matrix A in a range of cells, say A1:C3.
2. Go to the "Formulas" tab in the ribbon and click on "More Functions" in the "Functions Library" group.
3. In the "Function Arguments" dialog box, select the "Eigenvalue" function.
4. In the "Matrix" field, enter the range of cells containing the matrix A (A1:C3).
5. In the "Eigenvalue" field, enter the cell where you want to display the eigenvalue (say D1).
6. Click "OK" to calculate the eigenvalue.

The calculated eigenvalue will be displayed in cell D1.

To calculate the eigenvector, follow these steps:

1. Enter the matrix A in a range of cells, say A1:C3.
2. Go to the "Formulas" tab in the ribbon and click on "More Functions" in the "Functions Library" group.
3. In the "Function Arguments" dialog box, select the "Eigenvector" function.
4. In the "Matrix" field, enter the range of cells containing the matrix A (A1:C3).
5. In the "Eigenvector" field, enter the cell where you want to display the eigenvector (say E1).
6. Click "OK" to calculate the eigenvector.

The calculated eigenvector will be displayed in cell E1.

Interpreting the Results

Once you have calculated the eigenvalues and eigenvectors, you can interpret the results as follows:

• The eigenvalue represents the amount of change in the direction of the eigenvector.
• The eigenvector represents the direction of the change.

In the example above, the calculated eigenvalue is 3.618, and the calculated eigenvector is (0.577, 0.577, 0.577). This means that the direction of the change is along the line defined by the eigenvector, and the amount of change is 3.618 times the original value.

Gallery of Eigenvalue and Eigenvector Images

Eigenvalue and Eigenvector Image Gallery

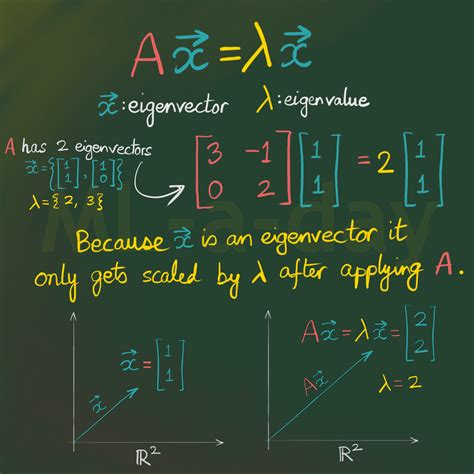
Conclusion

In conclusion, eigenvalues and eigenvectors are two fundamental concepts in linear algebra that have numerous applications in various fields. Calculating these values can be challenging, but Excel provides an efficient way to compute them using the "Eigenvalue" and "Eigenvector" functions. By following the steps outlined in this article, you can easily calculate the eigenvalues and eigenvectors of a square matrix and interpret the results.

We hope this article has been informative and helpful in understanding the concept of eigenvalues and eigenvectors. If you have any questions or need further clarification, please don't hesitate to ask.