Intro
Master the art of calculating area under a curve in Excel with ease. Learn how to use numerical integration methods, such as the trapezoidal rule and Simpsons rule, to accurately calculate area under curves, peaks, and surfaces. Simplify complex calculations and improve your data analysis skills with our step-by-step guide.
Calculating the area under a curve is a fundamental concept in mathematics and statistics, with numerous applications in fields such as physics, engineering, and economics. In Excel, this calculation can be performed using various methods, including numerical integration and approximation techniques. In this article, we will explore the different approaches to calculating the area under a curve in Excel, providing step-by-step instructions and practical examples to help you master this essential skill.
Understanding the Problem

The area under a curve can be calculated using various methods, including the trapezoidal rule, Simpson's rule, and numerical integration. The choice of method depends on the complexity of the curve, the desired level of accuracy, and the available data.
Trapezoidal Rule
The trapezoidal rule is a simple and widely used method for approximating the area under a curve. This method involves dividing the area into trapezoids and summing their areas. The formula for the trapezoidal rule is:Area ≈ (h/2) * (y0 + y1 + y2 + … + yn)
where h is the width of each trapezoid, and y0, y1, y2, …, yn are the values of the function at each point.
Excel Implementation
To implement the trapezoidal rule in Excel, follow these steps:
- Enter the data points in columns A and B, with the x-values in column A and the corresponding y-values in column B.
- Enter the formula
= (B2-B1)/2*(A2+A1)in cell C2, where B2 and B1 are the y-values, and A2 and A1 are the x-values. - Copy the formula down to the remaining cells in column C.
- Sum the values in column C to obtain the approximate area under the curve.
Simpson's Rule
Simpson's rule is another popular method for approximating the area under a curve. This method involves dividing the area into parabolic segments and summing their areas. The formula for Simpson's rule is:Area ≈ (h/3) * (y0 + 4*y1 + 2*y2 + 4*y3 + 2*y4 + … + yn)
where h is the width of each segment, and y0, y1, y2, …, yn are the values of the function at each point.
Excel Implementation

To implement Simpson's rule in Excel, follow these steps:
- Enter the data points in columns A and B, with the x-values in column A and the corresponding y-values in column B.
- Enter the formula
= (B2-B1)/3*(A2+A1+4*B2+2*B3)in cell C2, where B2 and B1 are the y-values, and A2 and A1 are the x-values. - Copy the formula down to the remaining cells in column C.
- Sum the values in column C to obtain the approximate area under the curve.
Numerical Integration
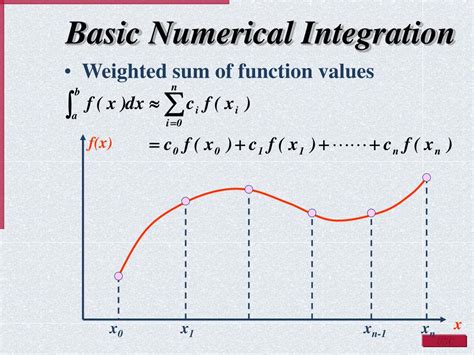
Numerical integration is a more advanced method for calculating the area under a curve. This method involves approximating the curve using a polynomial function and then integrating the polynomial.
To perform numerical integration in Excel, you can use the SCipy.integrate function or the NumericalIntegration add-in. Alternatively, you can use the SUMPRODUCT function to approximate the area under the curve.
Excel Implementation
To implement numerical integration in Excel using the `SUMPRODUCT` function, follow these steps:- Enter the data points in columns A and B, with the x-values in column A and the corresponding y-values in column B.
- Enter the formula
= SUMPRODUCT((A2:A10-A1:A9)/2,(B2:B10+B1:B9))in cell C1, where A2:A10 and B2:B10 are the x-values and y-values, respectively. - Press Enter to calculate the approximate area under the curve.
Excel Area Under Curve Calculation Made Easy Image Gallery





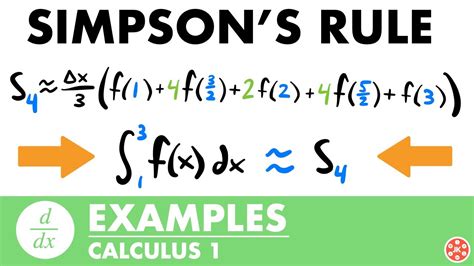
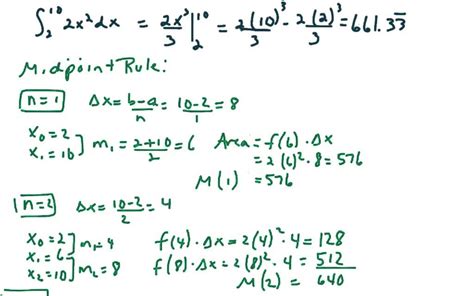

We hope this article has provided you with a comprehensive understanding of how to calculate the area under a curve in Excel. Whether you're a student, teacher, or professional, mastering this skill can help you solve a wide range of problems in mathematics, statistics, and other fields. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences in the comments section below, and don't forget to share this article with your friends and colleagues who may find it useful.
