Calculate Area Under Curve In Excel Made Easy

Calculating the area under a curve is a fundamental task in various fields such as physics, engineering, economics, and finance. It's a crucial step in understanding the behavior of a function or a dataset. While it may seem like a daunting task, Excel provides several ways to calculate the area under a curve, making it more accessible and efficient. In this article, we will explore the different methods to calculate the area under a curve in Excel, along with practical examples and tips.

Why Calculate the Area Under a Curve?

Before we dive into the methods, let's understand why calculating the area under a curve is important. The area under a curve can represent various quantities, such as:

• The accumulated value of a function over a given interval
• The probability of a random variable falling within a certain range
• The energy or work done by a system over a specific period
• The cumulative distribution of a dataset

In many cases, calculating the area under a curve is essential to gain insights into the behavior of a function or a dataset.

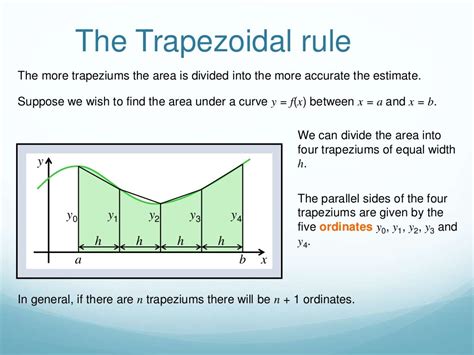
Method 1: Using the Trapezoidal Rule

The trapezoidal rule is a simple and widely used method to approximate the area under a curve. This method involves dividing the area into small trapezoids and summing up their individual areas.

To calculate the area under a curve using the trapezoidal rule in Excel:

1. Create a table with the x-values and corresponding y-values of the function.
2. Calculate the width of each trapezoid using the formula: (x2 - x1).
3. Calculate the area of each trapezoid using the formula: 0.5 * (y1 + y2) * width.
4. Sum up the areas of all trapezoids to get the total area under the curve.

Method 2: Using Simpson's Rule

Simpson's rule is another method to approximate the area under a curve. This method is more accurate than the trapezoidal rule, especially for smooth curves.

To calculate the area under a curve using Simpson's rule in Excel:

1. Create a table with the x-values and corresponding y-values of the function.
2. Calculate the width of each subinterval using the formula: (x2 - x1).
3. Calculate the area of each subinterval using the formula: (y1 + 4*y2 + y3) / 6 * width.
4. Sum up the areas of all subintervals to get the total area under the curve.

Method 3: Using Excel Functions

Excel provides several built-in functions to calculate the area under a curve, such as:

• AREA.CHART: This function calculates the area under a curve defined by a chart.
• SUMIF: This function calculates the sum of values in a range based on a condition.
• INT: This function calculates the definite integral of a function.

To calculate the area under a curve using Excel functions:

1. Create a chart of the function.
2. Use the AREA.CHART function to calculate the area under the curve.
3. Alternatively, use the SUMIF function to sum up the areas of individual intervals.

Method 4: Using VBA Macros

For more complex functions or large datasets, you can use VBA macros to calculate the area under a curve.

To calculate the area under a curve using VBA macros:

1. Create a VBA macro that defines the function and calculates the area under the curve.
2. Use the Integrate function to calculate the definite integral of the function.

Gallery of Area Under Curve Examples

Area Under Curve Examples

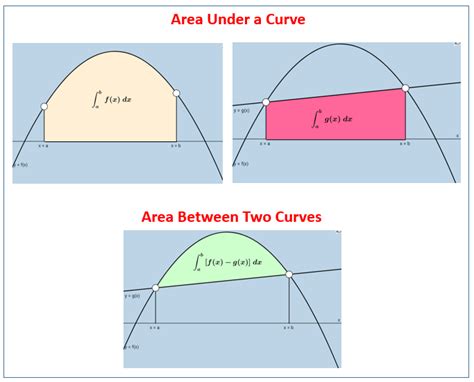
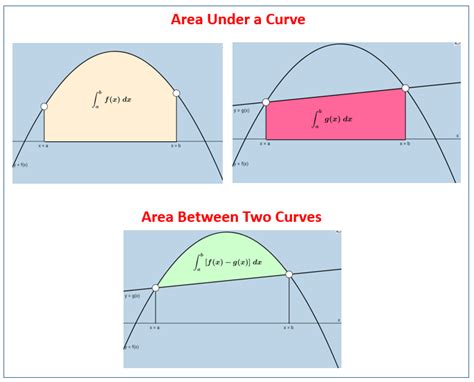
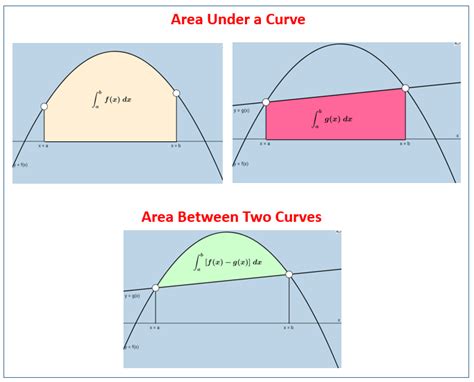
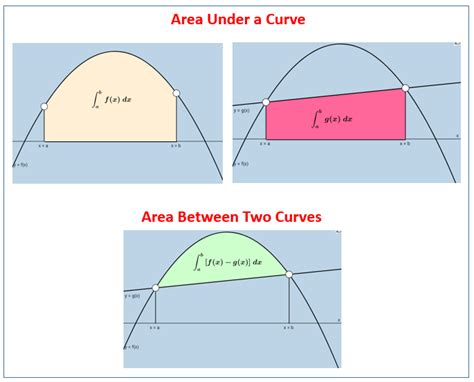
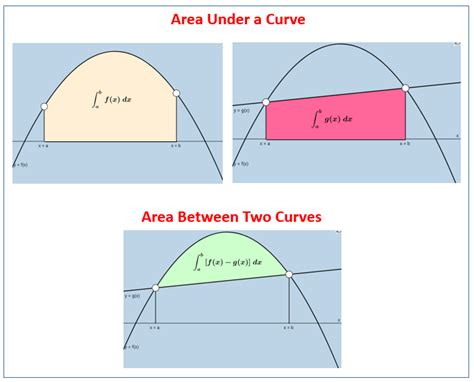
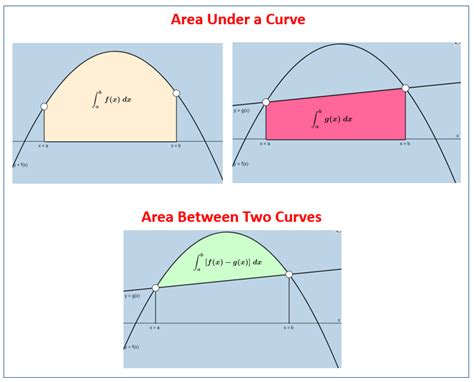
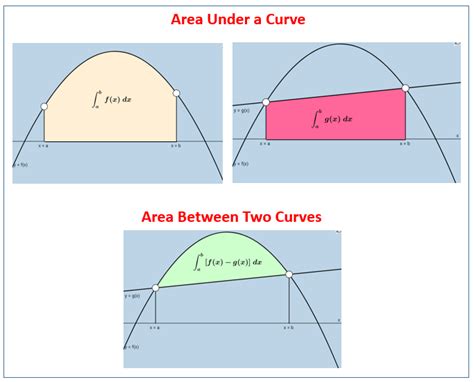
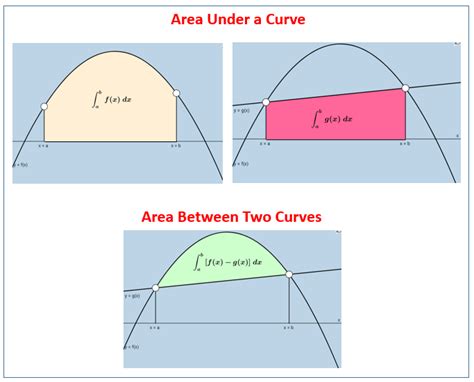
Conclusion

Calculating the area under a curve is a fundamental task in various fields, and Excel provides several methods to achieve this. From simple formulas to VBA macros, you can choose the method that best suits your needs. By following the examples and methods outlined in this article, you can efficiently calculate the area under a curve in Excel. Whether you're an engineer, economist, or finance professional, mastering this skill will help you make informed decisions and gain valuable insights into the behavior of functions and datasets.