Calculating Z scores in Excel is a crucial skill for any data analyst, statistician, or researcher. The Z score, also known as the standard score, is a measure of how many standard deviations an element is from the mean. In this article, we will walk you through a step-by-step guide on how to calculate Z scores in Excel.
The Importance of Z Scores
Z scores are essential in statistical analysis, as they allow us to compare data points from different datasets or distributions. By calculating the Z score, you can determine the probability of a data point occurring within a certain range. This is particularly useful in hypothesis testing, confidence intervals, and regression analysis.
When to Use Z Scores
Z scores are commonly used in various fields, including:
- Hypothesis testing: Z scores help you determine whether a sample mean is significantly different from a known population mean.
- Confidence intervals: Z scores are used to construct confidence intervals, which provide a range of values within which a population parameter is likely to lie.
- Regression analysis: Z scores can be used to standardize predictor variables, making it easier to compare their effects on the outcome variable.
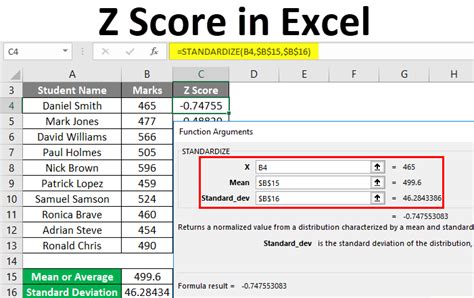
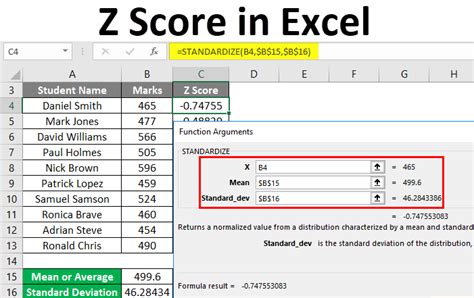
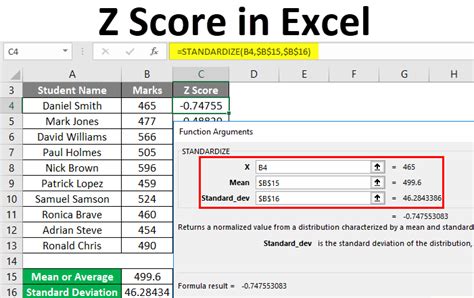
How to Calculate Z Scores in Excel
Now that we've covered the importance and applications of Z scores, let's dive into the step-by-step guide on how to calculate them in Excel.
Step 1: Enter Your Data
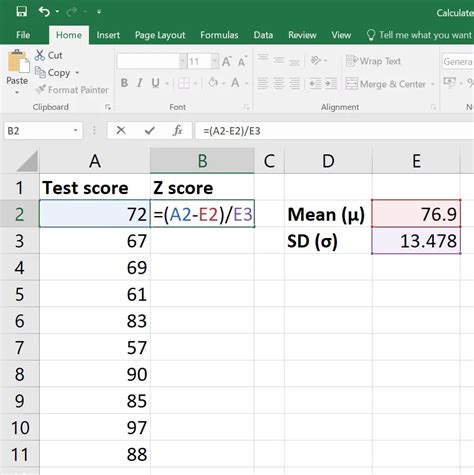
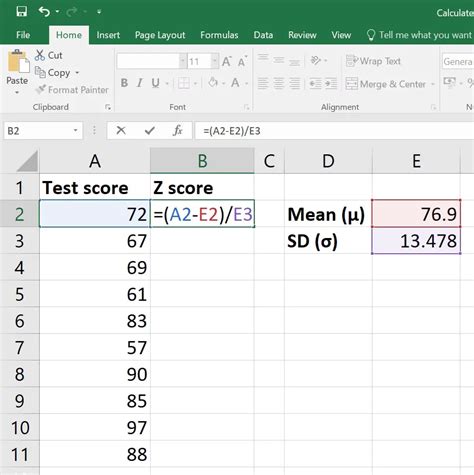
Enter your data into a column in Excel. For this example, we'll use the following dataset:
| Data |
|---|
| 23 |
| 25 |
| 19 |
| 21 |
| 24 |
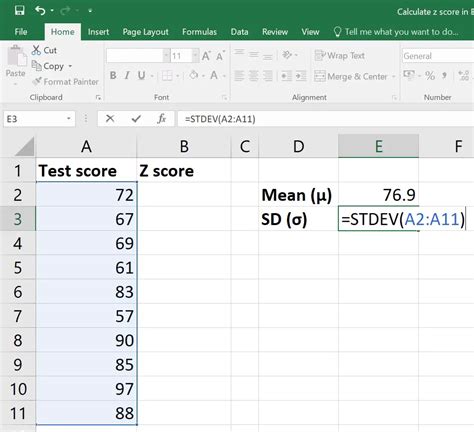
Step 2: Calculate the Mean
Calculate the mean of your dataset using the AVERAGE function.
| Formula | Result |
|---|---|
| =AVERAGE(A1:A5) | 22.4 |
Step 3: Calculate the Standard Deviation
Calculate the standard deviation of your dataset using the STDEV function.
| Formula | Result |
|---|---|
| =STDEV(A1:A5) | 2.24 |
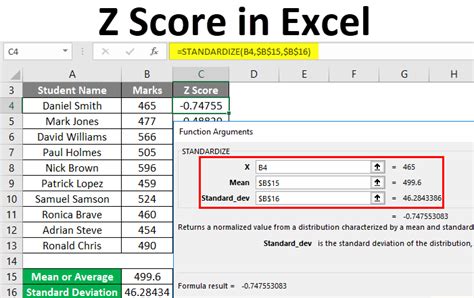
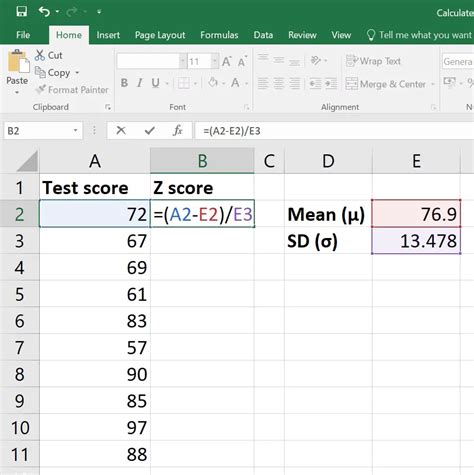
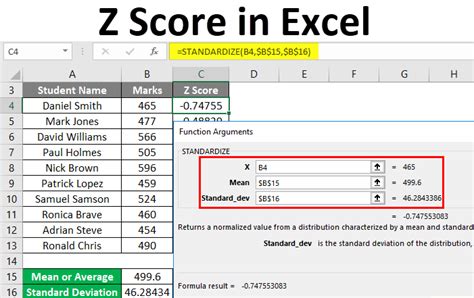
Step 4: Calculate the Z Score
Use the Z score formula to calculate the Z score for each data point:
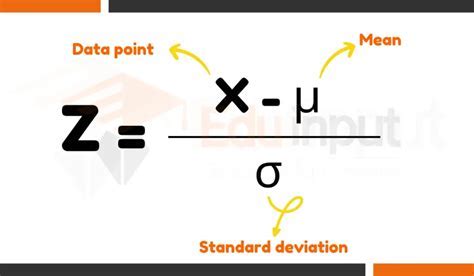
Z = (X - μ) / σ
Where:
- X is the data point
- μ is the mean
- σ is the standard deviation
Enter the formula into a new column:
| Formula | Result |
|---|---|
| =(A1-AVERAGE(A$1:A$5))/STDEV(A$1:A$5) | -0.44 |
Drag the formula down to apply it to the rest of the data points.
Step 5: Interpret the Results
The resulting Z scores will tell you how many standard deviations each data point is away from the mean. A Z score of 0 indicates that the data point is equal to the mean, while a positive Z score indicates that the data point is above the mean, and a negative Z score indicates that the data point is below the mean.
Tips and Variations
- Using the Z.TEST function: Excel also provides a built-in function, Z.TEST, which can be used to calculate the Z score. This function is particularly useful when working with large datasets.
- Standardizing multiple datasets: When working with multiple datasets, you can standardize each dataset separately and then compare the Z scores.
- Interpreting Z scores: When interpreting Z scores, keep in mind that a Z score of 1.96 or higher indicates that the data point is statistically significant at the 0.05 level.
Common Mistakes to Avoid
- Incorrect calculation of the mean or standard deviation: Make sure to calculate the mean and standard deviation correctly, as errors in these calculations can lead to incorrect Z scores.
- Forgetting to standardize the data: Standardizing the data is crucial when comparing Z scores from different datasets.
Gallery of Z Score Calculation
Z Score Calculation Image Gallery

Conclusion and Next Steps
Calculating Z scores in Excel is a straightforward process that can be accomplished using the steps outlined in this article. By following these steps and avoiding common mistakes, you can ensure accurate and reliable Z scores. Remember to standardize your data and interpret the results correctly to get the most out of your analysis.
Take the next step in your data analysis journey by exploring other statistical concepts and techniques. Share your experiences and insights in the comments below, and don't hesitate to ask for help if you have any questions or need further clarification. Happy analyzing!
