Excel Formula For Compound Interest With Annual Deposits Easily

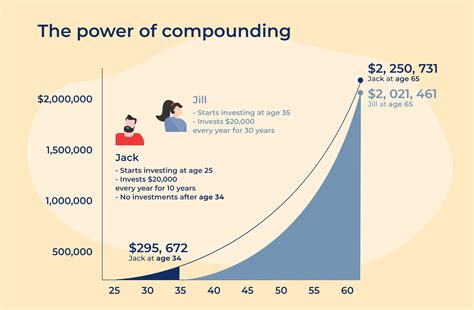
Investing wisely is a crucial aspect of securing your financial future. One of the most powerful tools for growing your wealth over time is compound interest. Compound interest is the concept of earning interest on both the principal amount and any accrued interest over time. When combined with annual deposits, it can create a snowball effect that dramatically increases your savings. However, calculating compound interest with annual deposits can be complex without the right tools. This is where Excel formulas come into play, offering a straightforward method to calculate and visualize your investments.

Understanding Compound Interest

Before diving into the Excel formula, it's essential to grasp the basics of compound interest. Compound interest is calculated on both the initial principal and the accumulated interest from previous periods. The frequency of compounding (e.g., monthly, quarterly, annually) affects how quickly your investment grows.

Factors Influencing Compound Interest

Several factors influence the outcome of compound interest:

Principal Amount: The initial amount of money deposited.
Interest Rate: The rate at which interest is earned.
Compounding Frequency: How often interest is compounded within a year.
Time: The number of years the money is invested.
Annual Deposits: Additional amounts deposited at regular intervals.

Excel Formula for Compound Interest with Annual Deposits

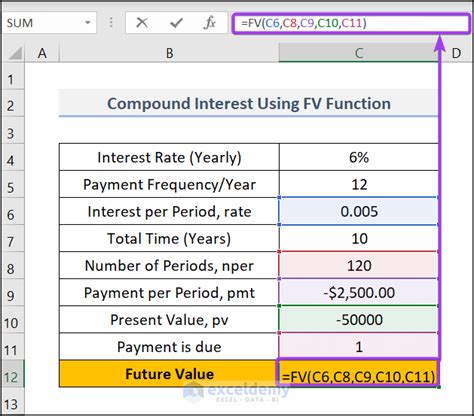
Excel offers a built-in function for calculating future values based on regular deposits and compound interest: the FV function. However, when you want to visualize and calculate the future value with more flexibility, especially with varying deposits, you might use a combination of formulas.

The general structure of the compound interest formula without considering deposits is:

A = P(1 + r/n)^(nt)

Where:

A = the future value of the investment/loan, including interest
P = principal investment amount (the initial deposit or loan amount)
r = annual interest rate (in decimal)
n = number of times that interest is compounded per year
t = time the money is invested or borrowed for, in years

For annual deposits, you would use the FV function:

FV(rate, nper, pmt, [pv], [type])

Where:

rate = interest rate per period
nper = total number of payment periods
pmt = payment made each period; it cannot change over the life of the annuity
[pv] = the present value, or the lump-sum amount, that a series of future payments is worth currently. If omitted, it is assumed to be 0, and you must include the pv argument for the formula to calculate.
[type] = when payments are due (0 = end of period, 1 = beginning of period). If omitted, type is assumed to be 0.

Practical Example

Assuming you start with a principal amount of $1,000, an annual interest rate of 5%, compounded annually, and you make an annual deposit of $500 for 10 years, the FV function would look like this:

=FV(0.05, 10, 500, -1000)

This formula calculates the future value of your investment based on the specified conditions.

Customizing the Formula

While the FV function provides a straightforward calculation, you might need to adjust the formula to fit specific scenarios, such as irregular deposits or varying interest rates. In such cases, breaking down the calculation into components and using a combination of formulas might be necessary.

Tips for Using Excel Formulas Effectively

Use Named Ranges: Instead of hardcoding values into your formula, use named ranges. This makes your formula easier to understand and adjust.
Reference Other Worksheets: If your data spans multiple worksheets, don't hesitate to reference them. This keeps your formulas dynamic and makes updates simpler.
Comment Your Formulas: For complex formulas, use Excel's comment feature to explain what the formula does. This is especially helpful for future reference or when collaborating.

Conclusion: Empowering Your Financial Future

Mastering the Excel formula for compound interest with annual deposits empowers you to make informed decisions about your investments. By understanding how to calculate and visualize the growth of your savings, you're better equipped to plan for the future. Remember, the key to successful investing is a combination of knowledge, patience, and the right tools.

Invite to Action

Share your own experiences with using Excel for financial planning in the comments below. How do you use compound interest calculations to guide your investment strategies? Let's start a conversation to help each other grow our financial literacy.