Mann Whitney Test In Excel: A Simple Step-By-Step Guide

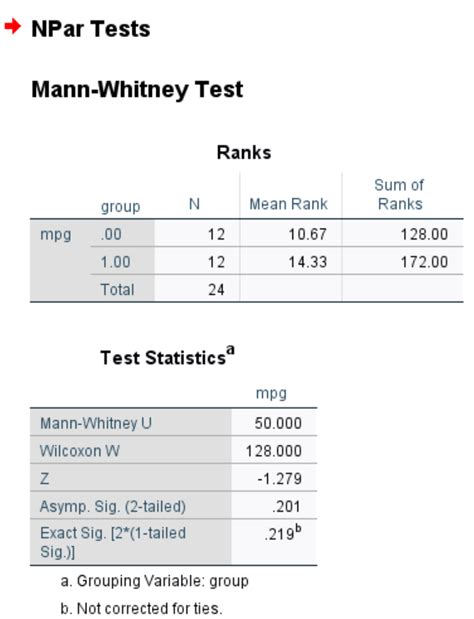
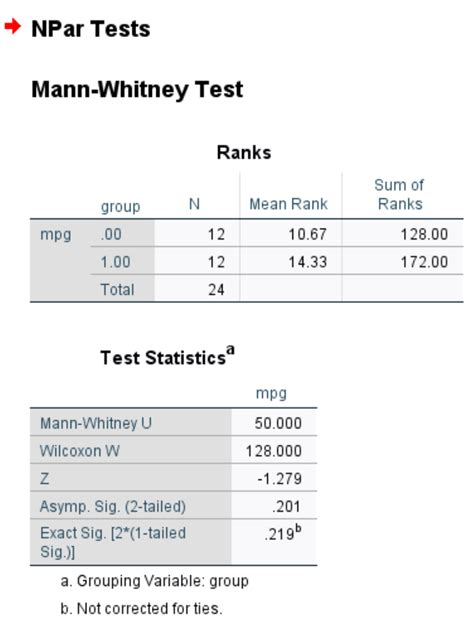
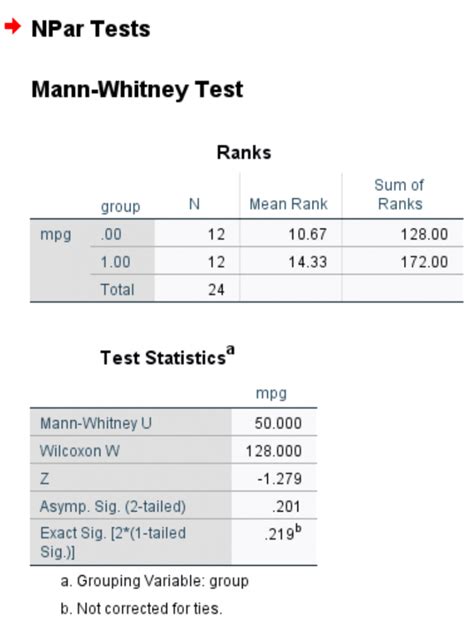
The Mann-Whitney test, also known as the Mann-Whitney U test or Wilcoxon rank-sum test, is a non-parametric statistical test used to compare two independent samples. It's a popular alternative to the t-test when the data doesn't meet the assumptions of normality or equal variances. In this article, we'll walk you through a simple step-by-step guide on how to perform a Mann-Whitney test in Excel.

Why Use the Mann-Whitney Test?

The Mann-Whitney test is a useful statistical tool when you need to compare two independent samples, and the data doesn't meet the assumptions of normality or equal variances. This test is particularly useful in situations where:

• The data is ordinal or ranked
• The data is not normally distributed
• The variances of the two groups are not equal

Assumptions of the Mann-Whitney Test

Before we dive into the step-by-step guide, it's essential to understand the assumptions of the Mann-Whitney test:

• The data should be independent and randomly sampled from the population
• The data should be ordinal or ranked
• The data should not be normally distributed

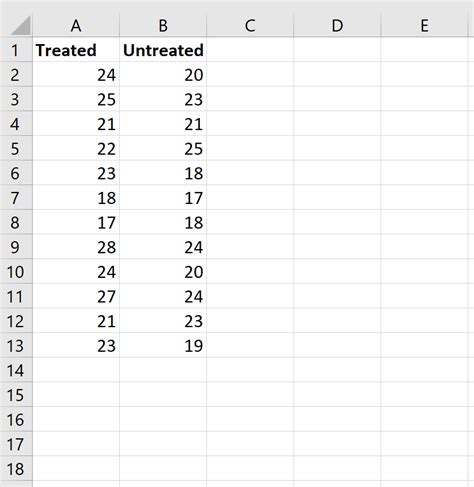
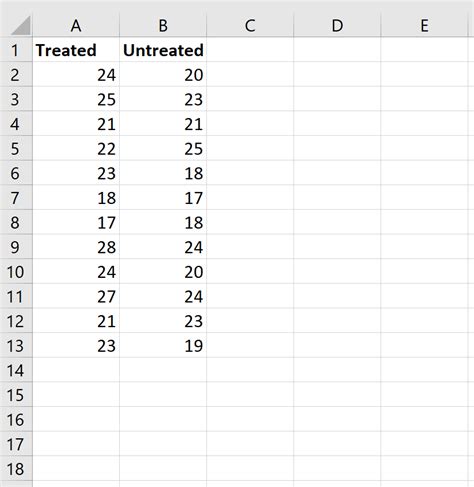
Step 1: Prepare Your Data

To perform a Mann-Whitney test in Excel, you'll need to prepare your data by following these steps:

• Enter your data into two separate columns in Excel, one for each group
• Make sure the data is clean and free of errors
• If your data is not already ranked or ordinal, you may need to rank it using the RANK function in Excel

Step 2: Use the Mann-Whitney Test Formula

The Mann-Whitney test formula is a bit complex, but don't worry, we'll break it down step by step. The formula is as follows:

U = n1 * n2 + (n1 * (n1 + 1)) / 2 - R1

Where:

• U is the Mann-Whitney test statistic
• n1 and n2 are the sample sizes of the two groups
• R1 is the sum of the ranks of the first group

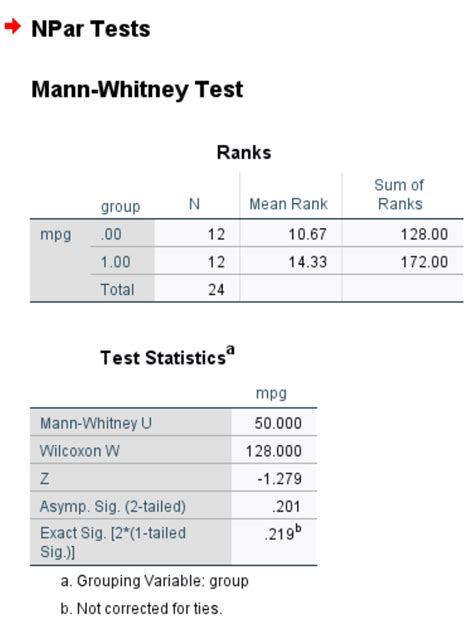
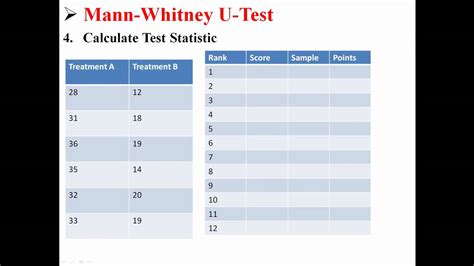
Step 3: Calculate the Ranks

To calculate the ranks, you can use the RANK function in Excel. Assuming your data is in columns A and B, you can use the following formula:

=RANK(A2,$A$2:$B$10)

This formula will rank the values in column A, with the smallest value getting a rank of 1.

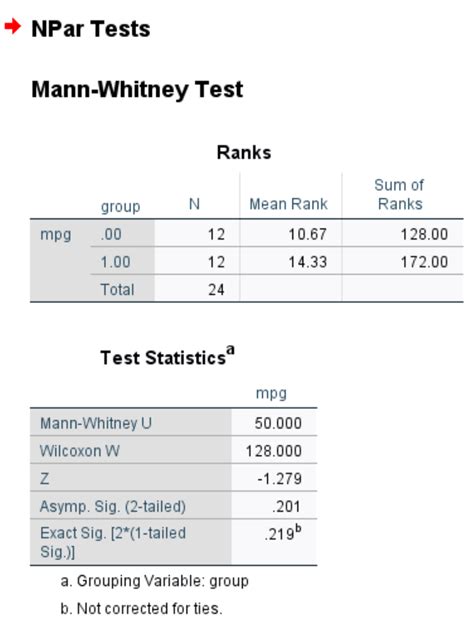
Step 4: Calculate the Mann-Whitney Test Statistic

Now that you have the ranks, you can calculate the Mann-Whitney test statistic using the formula:

U = n1 * n2 + (n1 * (n1 + 1)) / 2 - R1

Assuming your sample sizes are in cells C1 and C2, and your sum of ranks is in cell C3, you can use the following formula:

= C1 * C2 + (C1 * (C1 + 1)) / 2 - C3

Step 5: Determine the P-Value

The final step is to determine the p-value associated with the Mann-Whitney test statistic. You can use a Mann-Whitney test table or a statistical software package to determine the p-value.

In Excel, you can use the following formula to determine the p-value:

= 2 * (1 - NORMSINV(SQRT(U / (n1 * n2))))

This formula uses the inverse normal distribution function to determine the p-value.

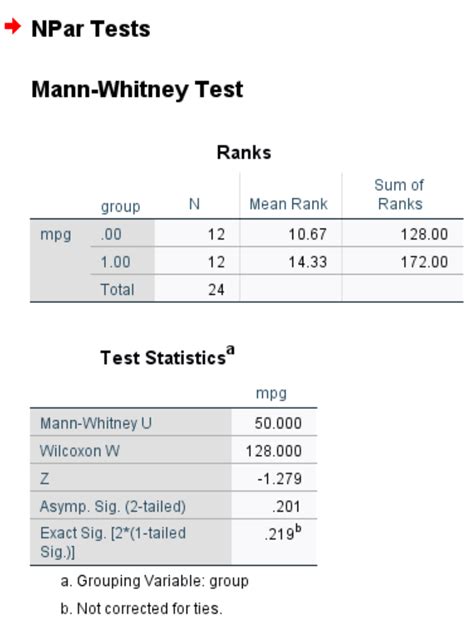
Interpreting the Results

The Mann-Whitney test produces a test statistic (U) and a p-value. The p-value indicates the probability of observing a test statistic as extreme or more extreme than the one you obtained, assuming that there is no real difference between the two groups.

If the p-value is less than your chosen significance level (usually 0.05), you can reject the null hypothesis and conclude that there is a statistically significant difference between the two groups.

Example

Suppose we want to compare the exam scores of two groups of students, one group taught using a traditional method and the other group taught using a new method. We collect the data and perform a Mann-Whitney test using the steps outlined above.

The results show a test statistic (U) of 25 and a p-value of 0.01. Since the p-value is less than our chosen significance level of 0.05, we can reject the null hypothesis and conclude that there is a statistically significant difference between the two groups.

Conclusion

In this article, we've provided a simple step-by-step guide on how to perform a Mann-Whitney test in Excel. We've covered the assumptions of the test, the steps to prepare your data, and the formula to calculate the test statistic and p-value.

By following these steps, you can easily perform a Mann-Whitney test in Excel and determine if there is a statistically significant difference between two independent samples.

Gallery of Mann Whitney Test Images

Mann Whitney Test Image Gallery

We hope you found this article helpful! Do you have any questions or comments about the Mann-Whitney test? Please leave them in the comments section below.