Intro
Master the Excel Mann Whitney U Test with ease. Learn how to perform this non-parametric test in Excel, comparing two independent samples to determine significant differences. Discover the step-by-step process, using real-world examples, and understand the tests assumptions, interpretation, and common pitfalls, ensuring accurate statistical analysis.
The Mann-Whitney U test is a powerful statistical tool used to compare two independent groups to determine if there are any significant differences between them. Despite its importance, many people find the test intimidating, especially when it comes to implementing it in Excel. In this article, we will break down the Mann-Whitney U test, explaining its underlying principles, and provide a step-by-step guide on how to perform it in Excel.
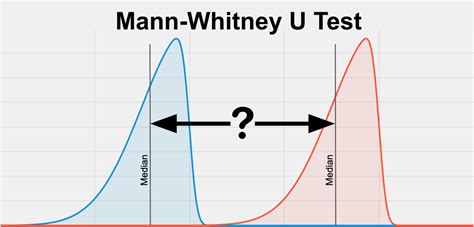
What is the Mann-Whitney U Test?
The Mann-Whitney U test, also known as the Wilcoxon rank-sum test, is a non-parametric test used to compare two independent groups. The test is used to determine if there are any significant differences between the two groups, without assuming any specific distribution of the data (e.g., normality). The test is commonly used in situations where the data is not normally distributed or when the sample size is small.
When to Use the Mann-Whitney U Test?
The Mann-Whitney U test is used in a variety of situations, including:
- Comparing the distribution of a continuous variable between two independent groups.
- Determining if there are any significant differences between two independent groups.
- Analyzing data that is not normally distributed.
How to Perform the Mann-Whitney U Test in Excel
Performing the Mann-Whitney U test in Excel is relatively straightforward. Here are the steps:
Step 1: Prepare Your Data
First, prepare your data by organizing it into two separate columns, each representing one of the groups you want to compare.
Step 2: Calculate the Ranks
Next, calculate the ranks for each data point in both groups. To do this, you can use the RANK.AVG function in Excel.
=RANK.AVG(A2,$A$2:$B$10)
This formula will assign a rank to each data point in the first column (A2), relative to all the data points in both columns ($A$2:$B$10).
Step 3: Calculate the U Statistic
Once you have the ranks, you can calculate the U statistic using the following formula:
=SUM(RANK.AVG(A2,$A$2:$B$10))-(n*(n+1))/2
This formula calculates the U statistic for the first group, where n is the number of data points in the first group.
Step 4: Calculate the Critical Value
To determine if the U statistic is significant, you need to calculate the critical value using a critical value table or a statistical software package.
Step 5: Interpret the Results
Finally, compare the calculated U statistic to the critical value. If the U statistic is less than the critical value, you reject the null hypothesis, indicating a significant difference between the two groups.
Interpretation and Assumptions
When interpreting the results of the Mann-Whitney U test, keep in mind the following:
- The test assumes that the data is independent and randomly sampled.
- The test does not assume any specific distribution of the data.
- The test is sensitive to tied ranks, which can affect the results.
Common Pitfalls and Misconceptions
When using the Mann-Whitney U test, be aware of the following common pitfalls and misconceptions:
- The test is not a substitute for a t-test or ANOVA. While it can be used to compare two groups, it is not as powerful as a t-test or ANOVA.
- The test is sensitive to outliers, which can affect the results.
- The test does not provide any information about the direction of the difference between the two groups.
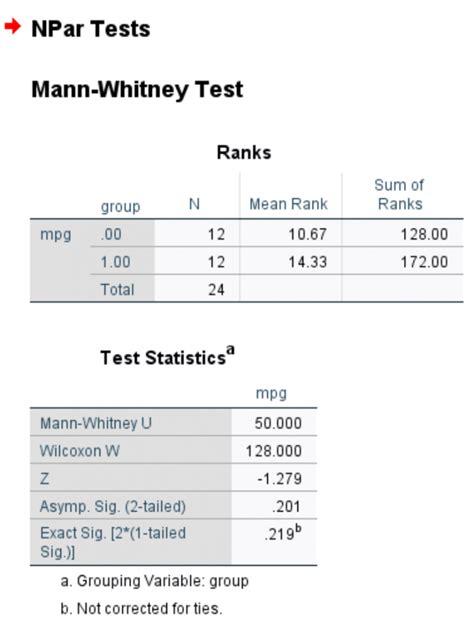
Gallery of Mann-Whitney U Test Images
Mann-Whitney U Test Image Gallery
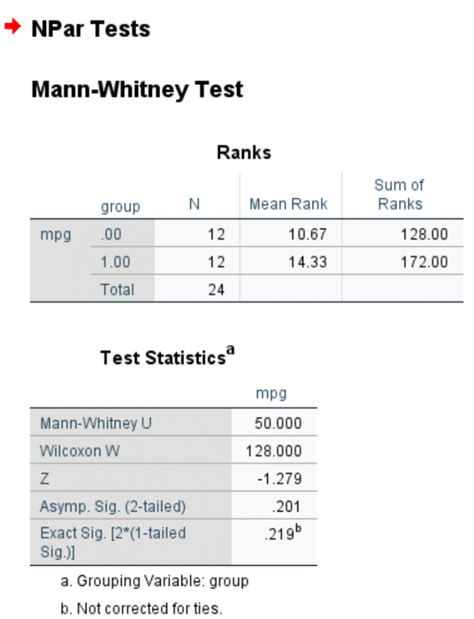
Frequently Asked Questions
Q: What is the difference between the Mann-Whitney U test and a t-test? A: The Mann-Whitney U test is a non-parametric test, while a t-test is a parametric test. The Mann-Whitney U test does not assume any specific distribution of the data, while a t-test assumes normality.
Q: Can I use the Mann-Whitney U test to compare more than two groups? A: No, the Mann-Whitney U test is used to compare two independent groups. If you want to compare more than two groups, you can use a Kruskal-Wallis H test.
Q: Is the Mann-Whitney U test sensitive to outliers? A: Yes, the Mann-Whitney U test is sensitive to outliers, which can affect the results.
We hope this article has helped you understand the Mann-Whitney U test and how to perform it in Excel. Remember to always check your data for normality and to consider using a t-test or ANOVA if your data meets the assumptions of those tests.