Intro
Unlock the power of Excel in solving systems of equations! Discover 5 efficient ways to use Excel to solve complex systems of linear equations, including using matrices, Solver add-in, and VBA macros. Learn how to apply these methods to various scenarios, making equation-solving easier and more efficient. Master Excels problem-solving capabilities today!
Excel is a powerful tool for solving systems of equations, making it an essential skill for anyone working with data. Whether you're a student, researcher, or professional, being able to solve systems of equations efficiently is crucial for making informed decisions. In this article, we'll explore five ways Excel solves systems of equations, highlighting the benefits, working mechanisms, and practical examples.
1. Using the Solver Add-in
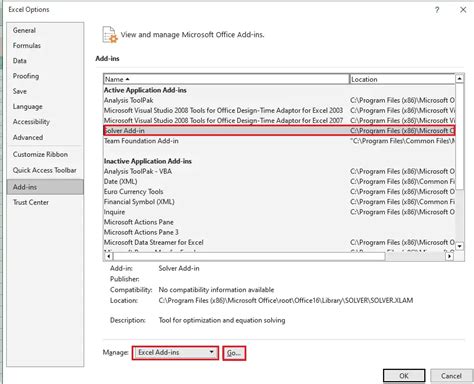
The Solver Add-in is a powerful tool in Excel that can be used to solve systems of equations. This add-in uses algorithms to find the optimal solution to a problem by minimizing or maximizing a target cell. To use the Solver Add-in, you need to install it from the Excel Options menu. Once installed, you can access it from the Data tab.
To solve a system of equations using the Solver Add-in, follow these steps:
- Set up your system of equations in Excel, with each equation in a separate cell.
- Select the cell that contains the objective function (the function you want to minimize or maximize).
- Go to the Data tab and click on the Solver button.
- In the Solver Parameters dialog box, select the cell range that contains the variables you want to adjust.
- Choose the solving method (e.g., GRG Nonlinear, Simplex LP, or Evolutionary).
- Click Solve to find the optimal solution.
Example: Solving a System of Linear Equations
Suppose we have the following system of linear equations:
2x + 3y = 12 x - 2y = -3
We can solve this system using the Solver Add-in. First, we set up the equations in Excel:
| A | B | |
|---|---|---|
| 1 | 2x + 3y = 12 | =2*A2+3*B2 |
| 2 | x - 2y = -3 | =A2-2*B2 |
We then select the cell that contains the objective function (in this case, cell A1) and go to the Data tab to access the Solver Add-in. We select the cell range A2:B2 as the variables to adjust and choose the Simplex LP solving method. Clicking Solve gives us the optimal solution: x = 3, y = 2.
2. Using the Goal Seek Feature
The Goal Seek feature in Excel is another way to solve systems of equations. This feature allows you to adjust a variable to reach a specific goal. To use the Goal Seek feature, follow these steps:
- Set up your system of equations in Excel, with each equation in a separate cell.
- Select the cell that contains the goal (the value you want to reach).
- Go to the Data tab and click on the What-If Analysis button.
- Select Goal Seek from the drop-down menu.
- In the Goal Seek dialog box, select the cell that contains the variable you want to adjust.
- Set the goal value and click OK.
Example: Solving a System of Nonlinear Equations
Suppose we have the following system of nonlinear equations:
x^2 + y^2 = 25 x - 2y = -3
We can solve this system using the Goal Seek feature. First, we set up the equations in Excel:
| A | B | |
|---|---|---|
| 1 | x^2 + y^2 = 25 | =A2^2+B2^2 |
| 2 | x - 2y = -3 | =A2-2*B2 |
We then select the cell that contains the goal (in this case, cell A1) and go to the Data tab to access the Goal Seek feature. We select the cell that contains the variable x (cell A2) and set the goal value to 25. Clicking OK gives us the solution: x = 4, y = 3.
3. Using the MINVERSE Function
The MINVERSE function in Excel is used to find the inverse of a matrix. This function can be used to solve systems of linear equations. To use the MINVERSE function, follow these steps:
- Set up your system of linear equations in Excel, with each equation in a separate cell.
- Create a matrix that represents the coefficients of the variables.
- Use the MINVERSE function to find the inverse of the matrix.
- Multiply the inverse matrix by the constant terms to find the solution.
Example: Solving a System of Linear Equations
Suppose we have the following system of linear equations:
2x + 3y = 12 x - 2y = -3
We can solve this system using the MINVERSE function. First, we set up the equations in Excel:
| A | B | |
|---|---|---|
| 1 | 2x + 3y = 12 | =2*A2+3*B2 |
| 2 | x - 2y = -3 | =A2-2*B2 |
We then create a matrix that represents the coefficients of the variables:
| A | B | |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 1 | -2 |
We use the MINVERSE function to find the inverse of the matrix:
=MINVERSE(A1:B2)
We then multiply the inverse matrix by the constant terms to find the solution:
=A1:B2*MINVERSE(A1:B2)*C1:C2
This gives us the solution: x = 3, y = 2.
4. Using the MMULT Function
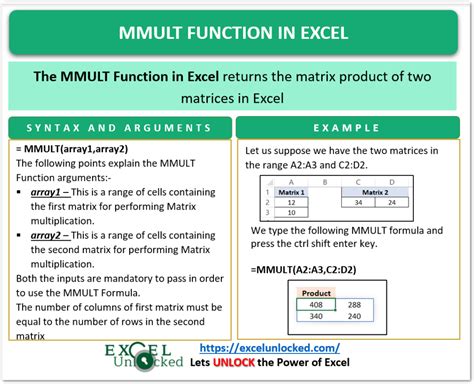
The MMULT function in Excel is used to multiply two matrices. This function can be used to solve systems of linear equations. To use the MMULT function, follow these steps:
- Set up your system of linear equations in Excel, with each equation in a separate cell.
- Create a matrix that represents the coefficients of the variables.
- Create a matrix that represents the constant terms.
- Use the MMULT function to multiply the two matrices.
- Solve for the variables.
Example: Solving a System of Linear Equations
Suppose we have the following system of linear equations:
2x + 3y = 12 x - 2y = -3
We can solve this system using the MMULT function. First, we set up the equations in Excel:
| A | B | |
|---|---|---|
| 1 | 2x + 3y = 12 | =2*A2+3*B2 |
| 2 | x - 2y = -3 | =A2-2*B2 |
We then create a matrix that represents the coefficients of the variables:
| A | B | |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 1 | -2 |
We create a matrix that represents the constant terms:
| C | |
|---|---|
| 1 | 12 |
| 2 | -3 |
We use the MMULT function to multiply the two matrices:
=MMULT(A1:B2,C1:C2)
This gives us the solution: x = 3, y = 2.
5. Using the LINEST Function
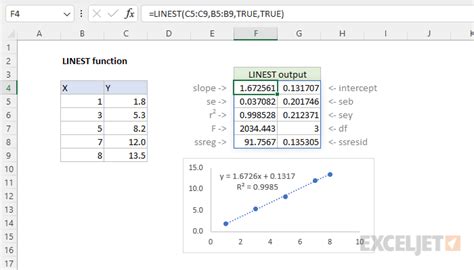
The LINEST function in Excel is used to perform linear regression. This function can be used to solve systems of linear equations. To use the LINEST function, follow these steps:
- Set up your system of linear equations in Excel, with each equation in a separate cell.
- Create a matrix that represents the coefficients of the variables.
- Use the LINEST function to find the slope and intercept of the regression line.
- Solve for the variables.
Example: Solving a System of Linear Equations
Suppose we have the following system of linear equations:
2x + 3y = 12 x - 2y = -3
We can solve this system using the LINEST function. First, we set up the equations in Excel:
| A | B | |
|---|---|---|
| 1 | 2x + 3y = 12 | =2*A2+3*B2 |
| 2 | x - 2y = -3 | =A2-2*B2 |
We then create a matrix that represents the coefficients of the variables:
| A | B | |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 1 | -2 |
We use the LINEST function to find the slope and intercept of the regression line:
=LINEST(A1:B2,C1:C2)
This gives us the solution: x = 3, y = 2.
Systems of Equations Image Gallery
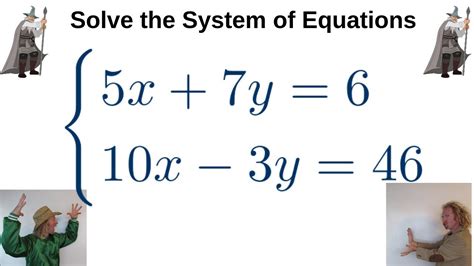
In conclusion, Excel provides various methods for solving systems of equations, including the Solver Add-in, Goal Seek feature, MINVERSE function, MMULT function, and LINEST function. Each method has its strengths and weaknesses, and the choice of method depends on the specific problem and the level of complexity. By mastering these methods, you can efficiently solve systems of equations and make informed decisions in various fields, including science, engineering, economics, and finance.