Intro
Understanding the Concept of Distance Between Two Points
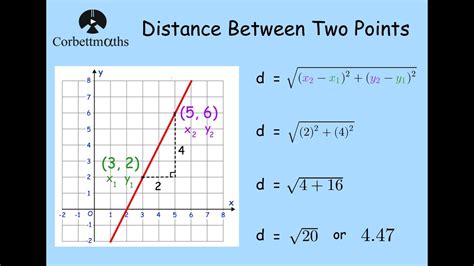
In mathematics and physics, calculating the distance between two points is a fundamental concept that has numerous applications in various fields, including geometry, trigonometry, engineering, and physics. Whether you're trying to find the distance between two cities on a map or the distance between two particles in a physical system, the concept of distance is crucial. In this article, we will explore five ways to find the distance between two points, including the use of formulas, coordinates, and real-world examples.
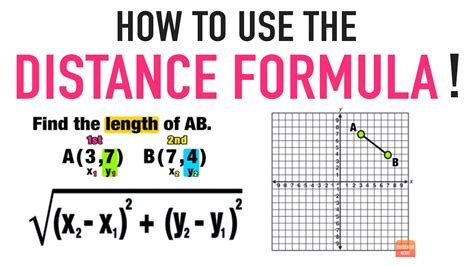
Method 1: Using the Distance Formula
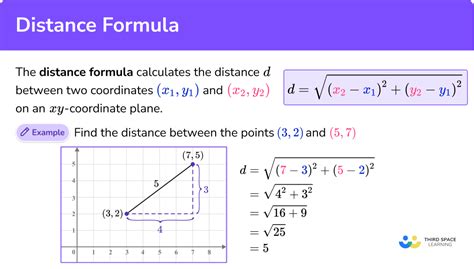
One of the most common methods for finding the distance between two points is to use the distance formula. This formula is based on the Pythagorean theorem and is widely used in mathematics and physics. The distance formula is:
d = √((x2 - x1)^2 + (y2 - y1)^2)
where d is the distance between the two points, (x1, y1) and (x2, y2) are the coordinates of the two points.
For example, if we want to find the distance between two points (3, 4) and (6, 8), we can plug in the values into the formula:
d = √((6 - 3)^2 + (8 - 4)^2) d = √(3^2 + 4^2) d = √(9 + 16) d = √25 d = 5
Advantages of Using the Distance Formula
- The distance formula is easy to use and apply.
- It is based on the Pythagorean theorem, which is a fundamental concept in mathematics.
- It can be used to find the distance between two points in a 2D or 3D space.
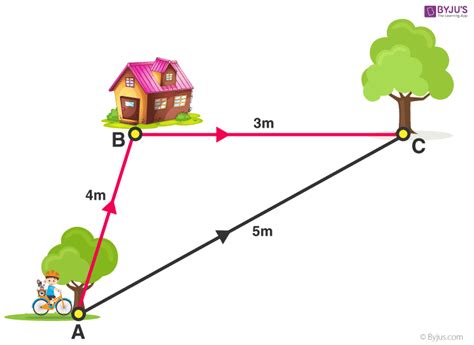
Method 2: Using Coordinates and the Pythagorean Theorem

Another way to find the distance between two points is to use coordinates and the Pythagorean theorem. This method is similar to the distance formula, but it involves breaking down the problem into smaller steps.
For example, if we want to find the distance between two points (2, 3) and (5, 6), we can use the Pythagorean theorem to find the distance:
- Find the horizontal distance between the two points: 5 - 2 = 3
- Find the vertical distance between the two points: 6 - 3 = 3
- Use the Pythagorean theorem to find the distance: √(3^2 + 3^2) = √(9 + 9) = √18
Advantages of Using Coordinates and the Pythagorean Theorem
- This method is useful when you need to find the distance between two points in a 2D or 3D space.
- It involves breaking down the problem into smaller steps, which can make it easier to understand and apply.
- It is based on the Pythagorean theorem, which is a fundamental concept in mathematics.
Method 3: Using Trigonometry
Trigonometry can also be used to find the distance between two points. This method involves using the sine, cosine, and tangent functions to find the distance.
For example, if we want to find the distance between two points (1, 2) and (4, 6), we can use the sine function to find the distance:
- Find the angle between the two points: θ = arctan(6/4)
- Use the sine function to find the distance: d = √(4^2 + 6^2) / sin(θ)
Advantages of Using Trigonometry
- Trigonometry can be used to find the distance between two points in a 2D or 3D space.
- It involves using the sine, cosine, and tangent functions, which are fundamental concepts in mathematics.
- It can be used to find the distance between two points in a triangular or circular motion.
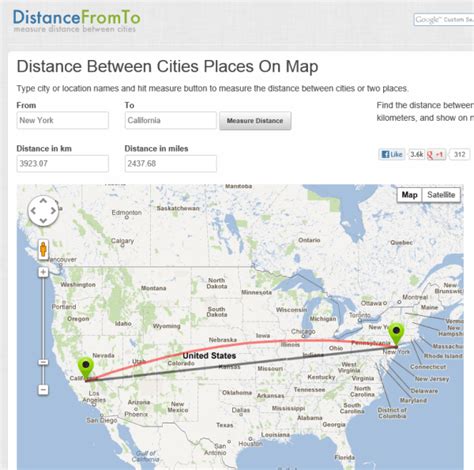
Method 4: Using Real-World Examples

Real-world examples can also be used to find the distance between two points. This method involves using everyday objects and situations to illustrate the concept of distance.
For example, if we want to find the distance between two cities, we can use a map to measure the distance. If we want to find the distance between two objects, we can use a ruler or a measuring tape to measure the distance.
Advantages of Using Real-World Examples
- Real-world examples can make the concept of distance more relatable and accessible.
- It involves using everyday objects and situations to illustrate the concept of distance.
- It can be used to find the distance between two points in a 2D or 3D space.
Method 5: Using Online Tools and Calculators

Online tools and calculators can also be used to find the distance between two points. This method involves using online resources to calculate the distance.
For example, if we want to find the distance between two cities, we can use an online mapping tool to calculate the distance. If we want to find the distance between two objects, we can use an online calculator to calculate the distance.
Advantages of Using Online Tools and Calculators
- Online tools and calculators can make it easy and quick to find the distance between two points.
- It involves using online resources to calculate the distance.
- It can be used to find the distance between two points in a 2D or 3D space.
Distance Between Two Points Image Gallery
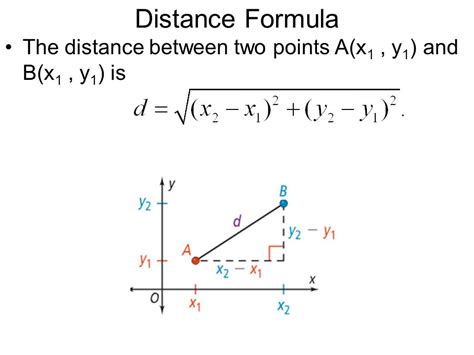





We hope this article has helped you understand the different ways to find the distance between two points. Whether you're using the distance formula, coordinates, trigonometry, real-world examples, or online tools and calculators, the concept of distance is a fundamental part of mathematics and physics. Remember to practice and apply these methods to become more proficient in finding the distance between two points.
