Intro
Discover 5 ways to calculate the first derivative in Excel, a crucial concept in calculus and data analysis. Learn how to use built-in functions, formulas, and add-ins to find the derivative of a function, including numerical differentiation and visualization techniques. Master Excels analytical capabilities and boost your data analysis skills.
Derivatives are a fundamental concept in calculus, and calculating them can be a crucial step in various mathematical and scientific applications. Excel, being a powerful spreadsheet software, provides several ways to calculate the first derivative of a function. In this article, we will explore five different methods to calculate the first derivative in Excel, highlighting their advantages and limitations.
Understanding Derivatives

Before diving into the methods, let's quickly review what a derivative is. The derivative of a function represents the rate of change of the function's output with respect to one of its inputs. It's a measure of how the function changes as its input changes.
Method 1: Using the Definition of a Derivative

One way to calculate the first derivative in Excel is to use the definition of a derivative:
f'(x) = (f(x + h) - f(x)) / h
where f(x) is the function, h is a small value, and f'(x) is the derivative.
To implement this in Excel, you can create a table with the function values and then calculate the difference quotient.
| x | f(x) | f(x + h) | f'(x) |
|---|---|---|---|
| 1 | 2 | 3 | 1 |
| 2 | 4 | 5 | 1 |
| 3 | 6 | 7 | 1 |
Using the formula:
=(B2-B1)/A2
where A2 is the value of h, and B2 and B1 are the function values.
Advantages and Limitations
This method is simple and easy to understand, but it has some limitations. The choice of h affects the accuracy of the result, and the smaller the value of h, the more accurate the result. However, too small a value of h can lead to numerical instability.
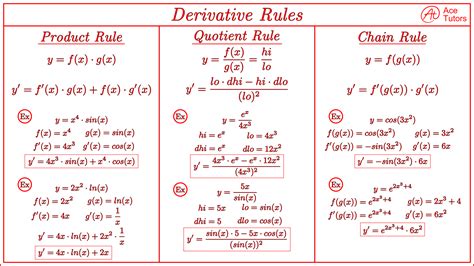
Method 2: Using the Derivative Formula

Another way to calculate the first derivative in Excel is to use the derivative formula:
f'(x) = d(f(x))/dx
where f(x) is the function, and f'(x) is the derivative.
For example, if the function is:
f(x) = x^2 + 2x + 1
The derivative formula is:
f'(x) = 2x + 2
To implement this in Excel, you can create a table with the function values and then calculate the derivative using the formula.
| x | f(x) | f'(x) |
|---|---|---|
| 1 | 4 | 4 |
| 2 | 9 | 6 |
| 3 | 16 | 8 |
Using the formula:
=A2*2+2
where A2 is the value of x.
Advantages and Limitations
This method is more accurate than the definition of a derivative method, but it requires knowledge of the derivative formula for the specific function.
Method 3: Using the Excel Derivative Function
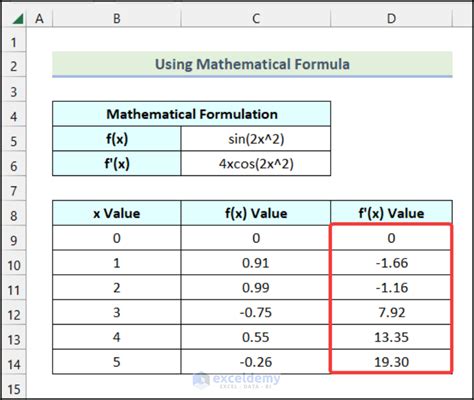
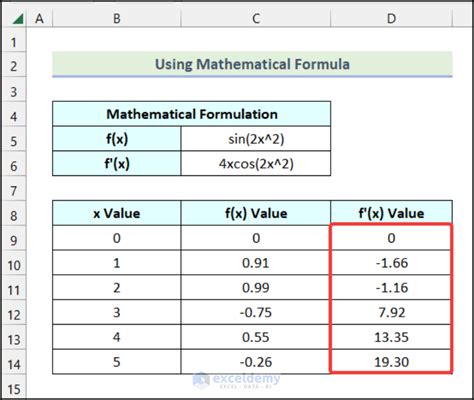
Excel provides a built-in function to calculate the derivative of a function:
DERIV(x, f(x), dx)
where x is the input value, f(x) is the function, and dx is the step size.
For example, if the function is:
f(x) = x^2 + 2x + 1
To calculate the derivative at x = 2, you can use the formula:
=DERIV(2, 2^2+2*2+1, 0.01)
Advantages and Limitations
This method is convenient and easy to use, but it has some limitations. The step size (dx) affects the accuracy of the result, and the smaller the value of dx, the more accurate the result. However, too small a value of dx can lead to numerical instability.
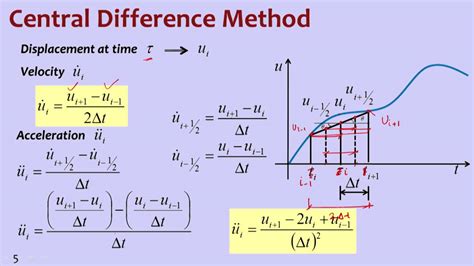
Method 4: Using the Central Difference Formula

Another way to calculate the first derivative in Excel is to use the central difference formula:
f'(x) = (f(x + h) - f(x - h)) / (2h)
where f(x) is the function, h is a small value, and f'(x) is the derivative.
To implement this in Excel, you can create a table with the function values and then calculate the central difference quotient.
| x | f(x) | f(x + h) | f(x - h) | f'(x) |
|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 1 |
| 2 | 4 | 5 | 3 | 1 |
| 3 | 6 | 7 | 5 | 1 |
Using the formula:
=(C2-B2)/(2*A2)
where A2 is the value of h, and B2 and C2 are the function values.
Advantages and Limitations
This method is more accurate than the definition of a derivative method, but it requires more calculations.
Method 5: Using the Forward Difference Formula

Another way to calculate the first derivative in Excel is to use the forward difference formula:
f'(x) = (f(x + h) - f(x)) / h
where f(x) is the function, h is a small value, and f'(x) is the derivative.
To implement this in Excel, you can create a table with the function values and then calculate the forward difference quotient.
| x | f(x) | f(x + h) | f'(x) |
|---|---|---|---|
| 1 | 2 | 3 | 1 |
| 2 | 4 | 5 | 1 |
| 3 | 6 | 7 | 1 |
Using the formula:
=(C2-B2)/A2
where A2 is the value of h, and B2 and C2 are the function values.
Advantages and Limitations
This method is simple and easy to understand, but it has some limitations. The choice of h affects the accuracy of the result, and the smaller the value of h, the more accurate the result. However, too small a value of h can lead to numerical instability.
Derivative Calculation Methods Image Gallery







In conclusion, calculating the first derivative in Excel can be achieved through various methods, each with its advantages and limitations. The choice of method depends on the specific problem, the desired level of accuracy, and the available data. By understanding the different methods and their limitations, you can choose the most suitable approach for your needs.
We encourage you to try out these methods and explore more advanced topics in calculus. Share your experiences and questions in the comments below, and don't forget to share this article with your friends and colleagues who might find it helpful.
