Discover the concept of Fixation Time On Hypergraph, exploring random walks, graph theory, and network analysis to understand its significance in complex systems and optimization problems.
The concept of fixation time on hypergraph has gained significant attention in recent years, particularly in the fields of computer science, mathematics, and network analysis. Fixation time refers to the amount of time it takes for a random walk on a hypergraph to reach a fixed point or a stationary distribution. Hypergraphs are a generalization of graphs, where edges can connect more than two vertices, making them a powerful tool for modeling complex networks and relationships.
The study of fixation time on hypergraph is crucial in understanding the behavior of random walks on these complex networks. Random walks are a fundamental concept in network analysis, and they have numerous applications in fields such as computer science, physics, and biology. By analyzing the fixation time on hypergraph, researchers can gain insights into the structural properties of the network, such as its connectivity, centrality, and community structure. This knowledge can be used to optimize network performance, predict the spread of information or diseases, and identify key nodes or clusters in the network.
The importance of fixation time on hypergraph cannot be overstated, as it has far-reaching implications for various fields of study. For instance, in computer science, understanding the fixation time on hypergraph can help improve the design of algorithms for network analysis, optimization, and machine learning. In physics, the study of fixation time on hypergraph can provide insights into the behavior of complex systems, such as social networks, biological systems, and transportation networks. Moreover, in biology, the analysis of fixation time on hypergraph can help researchers understand the spread of diseases, the behavior of complex biological systems, and the evolution of species.
Introduction to Hypergraph

A hypergraph is a mathematical structure that consists of a set of vertices and a set of edges, where each edge can connect more than two vertices. Hypergraphs are a generalization of graphs, where edges are limited to connecting only two vertices. The study of hypergraphs has gained significant attention in recent years, particularly in the fields of computer science, mathematics, and network analysis. Hypergraphs have numerous applications in fields such as data mining, machine learning, and network optimization.
Key Concepts in Hypergraph
Hypergraphs have several key concepts that are essential for understanding their structure and behavior. Some of the key concepts in hypergraph include: * Vertices: The basic building blocks of a hypergraph, which represent the nodes or entities in the network. * Edges: The connections between vertices, which can connect more than two vertices. * Hyperedges: A set of edges that connect a subset of vertices. * Incidence matrix: A matrix that represents the relationships between vertices and edges. * Adjacency matrix: A matrix that represents the relationships between vertices.Fixation Time on Hypergraph
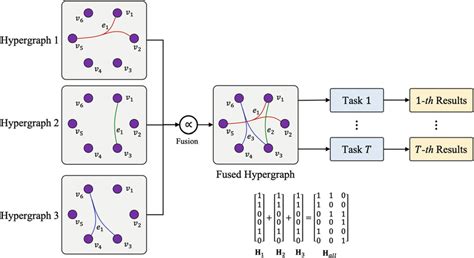
Fixation time on hypergraph refers to the amount of time it takes for a random walk on a hypergraph to reach a fixed point or a stationary distribution. The study of fixation time on hypergraph is crucial in understanding the behavior of random walks on these complex networks. Random walks are a fundamental concept in network analysis, and they have numerous applications in fields such as computer science, physics, and biology.
Calculating Fixation Time on Hypergraph
Calculating the fixation time on hypergraph involves several steps, including: 1. Defining the hypergraph structure: The first step is to define the hypergraph structure, including the vertices, edges, and hyperedges. 2. Defining the random walk: The next step is to define the random walk on the hypergraph, including the transition probabilities and the starting vertex. 3. Calculating the fixation time: The final step is to calculate the fixation time, which can be done using various methods, such as Monte Carlo simulations or analytical solutions.Applications of Fixation Time on Hypergraph

The study of fixation time on hypergraph has numerous applications in various fields, including:
- Computer science: Understanding the fixation time on hypergraph can help improve the design of algorithms for network analysis, optimization, and machine learning.
- Physics: The study of fixation time on hypergraph can provide insights into the behavior of complex systems, such as social networks, biological systems, and transportation networks.
- Biology: The analysis of fixation time on hypergraph can help researchers understand the spread of diseases, the behavior of complex biological systems, and the evolution of species.
Real-World Examples of Fixation Time on Hypergraph
Some real-world examples of fixation time on hypergraph include: * Social networks: The study of fixation time on hypergraph can help understand the spread of information or diseases on social networks. * Biological systems: The analysis of fixation time on hypergraph can help researchers understand the behavior of complex biological systems, such as gene regulatory networks or protein-protein interaction networks. * Transportation networks: The study of fixation time on hypergraph can help optimize the design of transportation networks, such as traffic flow or logistics.Future Directions for Fixation Time on Hypergraph

The study of fixation time on hypergraph is a rapidly evolving field, with numerous future directions and applications. Some potential future directions include:
- Developing new algorithms for calculating fixation time on hypergraph.
- Applying the concept of fixation time on hypergraph to real-world problems, such as optimizing network performance or predicting the spread of diseases.
- Integrating the study of fixation time on hypergraph with other fields, such as machine learning or data mining.
Challenges and Opportunities for Fixation Time on Hypergraph
Some challenges and opportunities for fixation time on hypergraph include: * Developing efficient algorithms for calculating fixation time on large-scale hypergraphs. * Applying the concept of fixation time on hypergraph to real-world problems, such as optimizing network performance or predicting the spread of diseases. * Integrating the study of fixation time on hypergraph with other fields, such as machine learning or data mining.Fixation Time on Hypergraph Image Gallery






We hope this article has provided a comprehensive overview of the concept of fixation time on hypergraph. The study of fixation time on hypergraph is a rapidly evolving field, with numerous applications and future directions. We encourage readers to explore this topic further and to share their thoughts and insights in the comments section below. Additionally, we invite readers to share this article with others who may be interested in this topic, and to follow us for more articles on related topics. By working together, we can advance our understanding of complex networks and develop new technologies and applications that can benefit society as a whole.
