Learn Algebra Fast Today

Learning algebra can seem like a daunting task, but with the right approach, it can be a rewarding and enjoyable experience. Algebra is a fundamental branch of mathematics that deals with variables and their relationships, and it is a crucial tool for problem-solving in various fields, including science, engineering, and economics. In this article, we will explore the importance of algebra, its benefits, and provide tips and strategies for learning algebra fast.

Algebra is a powerful tool that helps us model real-world problems, analyze data, and make informed decisions. It is used in a wide range of applications, from simple calculations to complex simulations. For instance, algebra is used in computer science to develop algorithms, in physics to describe the laws of motion, and in finance to analyze market trends. The ability to understand and apply algebraic concepts is essential for success in these fields.

Moreover, learning algebra can have a significant impact on our cognitive abilities, such as problem-solving, critical thinking, and analytical reasoning. Algebra requires us to think logically, make connections between different concepts, and visualize relationships between variables. These skills are transferable to other areas of life, including personal and professional development. By learning algebra, we can improve our ability to approach complex problems, break them down into manageable parts, and find creative solutions.

Introduction to Algebra

Algebra is a vast and fascinating field that encompasses various topics, including equations, functions, graphs, and matrices. To learn algebra fast, it is essential to start with the basics and build a strong foundation. This includes understanding the concept of variables, constants, and mathematical operations, such as addition, subtraction, multiplication, and division. We must also learn to manipulate algebraic expressions, solve equations, and graph functions.

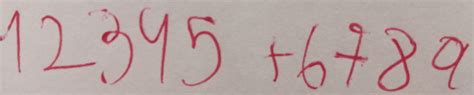
Benefits of Learning Algebra

The benefits of learning algebra are numerous and far-reaching. Algebra helps us develop problem-solving skills, critical thinking, and analytical reasoning. It also improves our ability to communicate complex ideas, think logically, and make informed decisions. Moreover, algebra is a fundamental tool for success in various fields, including science, engineering, economics, and computer science.

Some of the key benefits of learning algebra include:

Improved problem-solving skills
Enhanced critical thinking and analytical reasoning
Better communication skills
Increased career opportunities
Improved cognitive abilities

How to Learn Algebra Fast

To learn algebra fast, we must adopt a strategic approach that includes practice, review, and application. Here are some tips and strategies to help us learn algebra quickly: * Start with the basics: Understand the concept of variables, constants, and mathematical operations. * Practice regularly: Solve equations, graph functions, and manipulate algebraic expressions. * Review and reflect: Regularly review what we have learned and reflect on our progress. * Apply algebra to real-world problems: Use algebra to model and solve real-world problems. * Seek help when needed: Don't hesitate to ask for help when we are struggling with a concept.

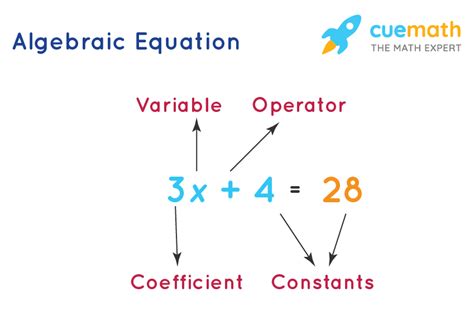
Algebraic Concepts

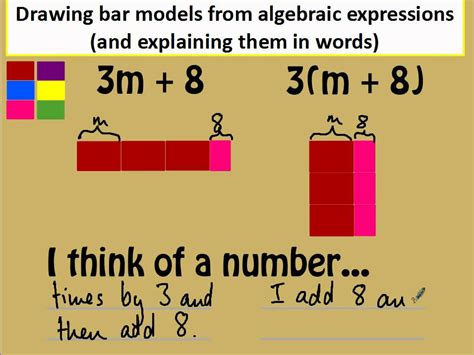
Algebraic concepts are the building blocks of algebra, and they include variables, constants, and mathematical operations. We must understand how to manipulate algebraic expressions, solve equations, and graph functions. Some of the key algebraic concepts include: * Variables: Letters or symbols that represent unknown values. * Constants: Numbers that do not change value. * Mathematical operations: Addition, subtraction, multiplication, and division. * Equations: Statements that express the equality of two algebraic expressions. * Functions: Relations between variables that assign a unique output to each input.

Algebraic Equations

Algebraic equations are statements that express the equality of two algebraic expressions. To solve an equation, we must isolate the variable, which involves adding, subtracting, multiplying, or dividing both sides of the equation by the same value. We must also learn to solve systems of equations, which involve two or more equations with two or more variables.

Some of the key techniques for solving algebraic equations include:

Adding or subtracting the same value to both sides of the equation.
Multiplying or dividing both sides of the equation by the same value.
Using inverse operations to isolate the variable.
Graphing the equation to visualize the solution.

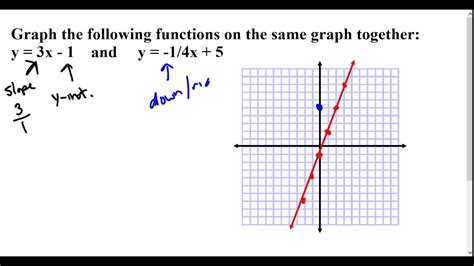
Graphing Functions

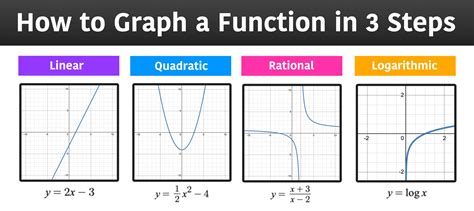
Graphing functions is a powerful tool for visualizing relationships between variables. We must learn to graph linear and non-linear functions, including quadratic, polynomial, and rational functions. Graphing functions helps us understand the behavior of the function, including its domain, range, and intercepts.

Some of the key concepts in graphing functions include:

Domain: The set of all possible input values.
Range: The set of all possible output values.
Intercepts: The points where the graph intersects the x-axis or y-axis.
Slope: The rate of change of the function.

Real-World Applications of Algebra

Algebra has numerous real-world applications, including science, engineering, economics, and computer science. We must learn to apply algebraic concepts to model and solve real-world problems. Some examples of real-world applications of algebra include: * Physics: Algebra is used to describe the laws of motion, including velocity, acceleration, and force. * Engineering: Algebra is used to design and optimize systems, including electronic circuits and mechanical systems. * Economics: Algebra is used to model economic systems, including supply and demand, and to analyze market trends. * Computer Science: Algebra is used to develop algorithms, including sorting and searching algorithms.

Conclusion and Next Steps

In conclusion, learning algebra is a rewarding and challenging experience that requires dedication, practice, and application. By understanding the importance of algebra, its benefits, and how to learn it quickly, we can develop a strong foundation in algebra and improve our problem-solving skills, critical thinking, and analytical reasoning.

To further develop our skills in algebra, we must continue to practice, review, and apply algebraic concepts to real-world problems. We must also seek help when needed and stay motivated to overcome challenges and obstacles.

Gallery of Algebraic Concepts

Algebra Image Gallery

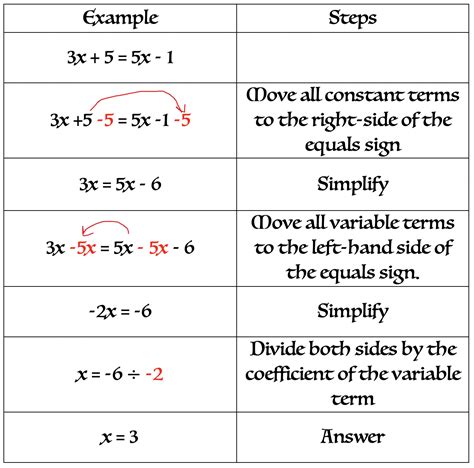
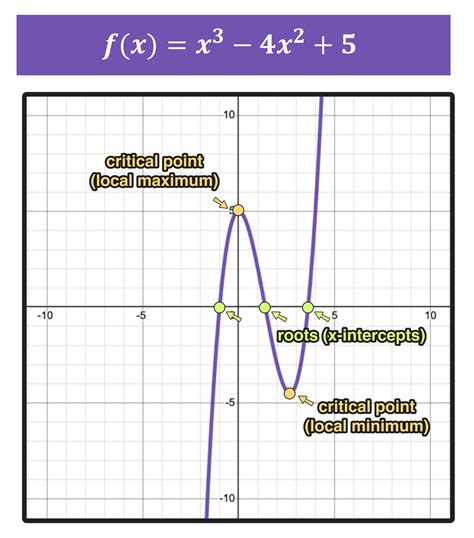
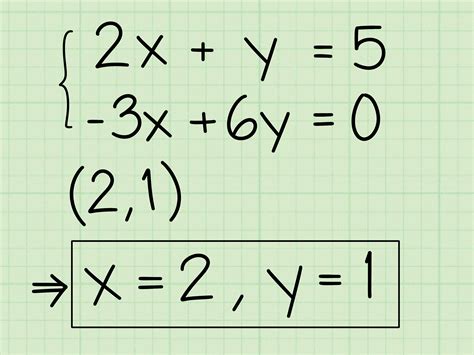
We hope this article has provided valuable insights and tips for learning algebra fast. We encourage readers to share their experiences, ask questions, and provide feedback in the comments section below. By working together, we can develop a deeper understanding of algebra and its applications, and improve our problem-solving skills, critical thinking, and analytical reasoning.