3 Ways To Calculate Area Under A Curve In Excel

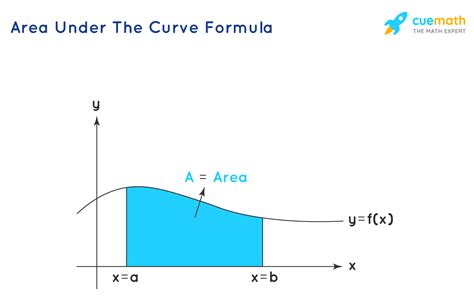
Calculating the area under a curve is a fundamental concept in mathematics and statistics, particularly in fields like engineering, economics, and data analysis. While it can be done manually, using a software tool like Microsoft Excel can greatly simplify the process. In this article, we will explore three different methods to calculate the area under a curve in Excel.

Why is calculating the area under a curve important?

Calculating the area under a curve is essential in various applications, such as:

• Probability and statistics: The area under a probability distribution curve represents the probability of a specific event occurring.
• Engineering: The area under a curve can represent the accumulation of a quantity over time or space, such as the accumulation of stress on a material.
• Economics: The area under a demand curve represents the total revenue or consumer surplus.

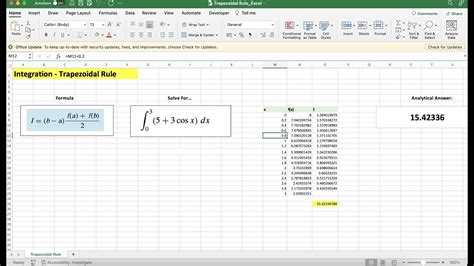
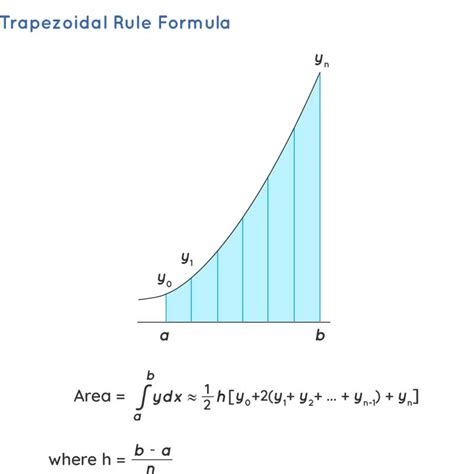
Method 1: Using the Trapezoidal Rule

The Trapezoidal Rule is a simple and effective method to approximate the area under a curve. It works by dividing the area under the curve into small trapezoids and summing up their areas.

To apply the Trapezoidal Rule in Excel:

1. Prepare your data by creating a table with the x-values in one column and the corresponding y-values in another column.
2. Calculate the width of each trapezoid by subtracting the x-values.
3. Calculate the area of each trapezoid using the formula: (y1 + y2) / 2 * width.
4. Sum up the areas of all trapezoids to get the approximate area under the curve.

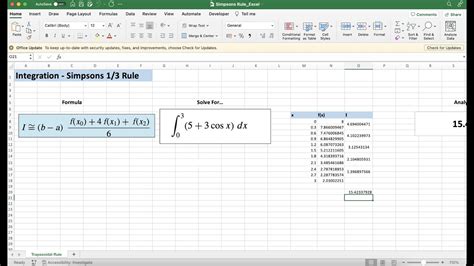
Method 2: Using the Simpson's Rule

Simpson's Rule is another method to approximate the area under a curve. It is more accurate than the Trapezoidal Rule, especially for smooth curves.

To apply Simpson's Rule in Excel:

1. Prepare your data by creating a table with the x-values in one column and the corresponding y-values in another column.
2. Calculate the width of each subinterval by subtracting the x-values.
3. Calculate the area of each subinterval using the formula: (y1 + 4*y2 + y3) / 6 * width.
4. Sum up the areas of all subintervals to get the approximate area under the curve.

Method 3: Using the SCipy library and xlwings

If you need a more accurate and robust method, you can use the SCipy library in Python and xlwings to integrate it with Excel.

To use this method:

1. Install SCipy and xlwings in your Python environment.
2. Import the SCipy library and xlwings in your Python script.
3. Define a function to calculate the area under the curve using SCipy's quad function.
4. Use xlwings to interact with Excel and calculate the area under the curve.

Gallery of Calculating Area Under Curve

Area Under Curve Image Gallery

Conclusion and Next Steps

Calculating the area under a curve is an essential skill in various fields, and Excel provides a convenient platform to do so. The three methods discussed in this article can help you approximate the area under a curve with varying degrees of accuracy. By following these steps and exploring the gallery of images, you can become proficient in calculating the area under a curve in Excel.

We want to hear from you!

Have you used any of these methods to calculate the area under a curve in Excel? Share your experiences, tips, and tricks in the comments below. Don't forget to share this article with your colleagues and friends who might find it helpful.

Additional Resources

• Microsoft Excel Documentation: Trapezoidal Rule
• Microsoft Excel Documentation: Simpson's Rule
• SCipy Documentation: quad function
• xlwings Documentation: Installation

Note: The images used in this article are for illustrative purposes only and are not intended to be used for commercial purposes.