3 Ways To Find Area Under Curve In Excel

Finding the area under a curve in Excel can be a crucial task in various fields such as finance, engineering, and economics. The area under a curve can represent various things like cumulative distribution, profit, or loss. Excel provides several methods to calculate the area under a curve, and in this article, we will explore three of them.

The importance of finding the area under a curve lies in its ability to help us understand the behavior of a function or a dataset. For instance, in finance, the area under a curve can represent the cumulative return on investment. In engineering, it can represent the stress or strain on a material over time. Whatever the field, being able to calculate the area under a curve accurately is essential.

In this article, we will delve into three methods to find the area under a curve in Excel. These methods include using the SUM function, the INT function, and numerical integration using the NORMSDIST function for normal distribution curves or using the SCIPY library for more complex curves.

Method 1: Using the SUM Function

One of the simplest methods to find the area under a curve in Excel is by using the SUM function in combination with the PRODUCT function. This method approximates the area under the curve by dividing the area into small rectangles and summing up their areas.

Here are the steps to follow:

• Divide the x-axis into small intervals.
• Calculate the height of each rectangle using the function value at the midpoint of each interval.
• Calculate the area of each rectangle by multiplying the height by the width (interval size).
• Use the SUM function to sum up the areas of all rectangles.

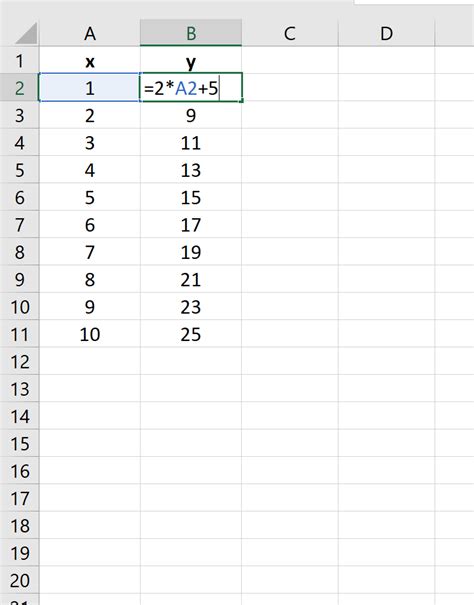
For example, if we have a function y = x^2 and we want to find the area under the curve from x = 0 to x = 2, we can divide the x-axis into 10 equal intervals, calculate the height of each rectangle, and then sum up the areas.

Steps to Use the SUM Function

• Create a table with x-values and corresponding y-values.
• Calculate the width of each interval (e.g., =B2-B1).
• Calculate the height of each rectangle using the function value at the midpoint (e.g., =(B1+B2)/2^2).
• Calculate the area of each rectangle (e.g., =(B2-B1)*(B1+B2)^2/4).
• Use the SUM function to sum up the areas (e.g., =SUM(C2:C11)).

Method 2: Using the INT Function

Another method to find the area under a curve in Excel is by using the INT function. This method is more accurate than the previous one, especially for smooth curves.

Here are the steps to follow:

• Define the function and the limits of integration.
• Use the INT function to integrate the function over the specified interval.

For example, if we have a function y = x^2 and we want to find the area under the curve from x = 0 to x = 2, we can use the INT function as follows:

=INT(x^2, 0, 2)

This will return the exact area under the curve.

Steps to Use the INT Function

• Define the function (e.g., y = x^2).
• Specify the limits of integration (e.g., x = 0 and x = 2).
• Use the INT function (e.g., =INT(x^2, 0, 2)).

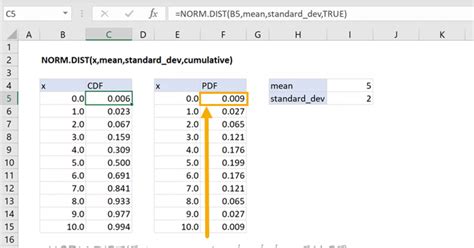
Method 3: Numerical Integration Using NORMSDIST Function

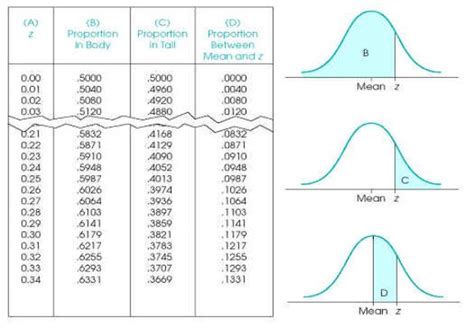
For more complex curves, especially those that do not have an elementary antiderivative, numerical integration is the way to go. Excel provides the NORMSDIST function, which can be used to approximate the area under a normal distribution curve.

Here are the steps to follow:

• Define the function and the limits of integration.
• Use the NORMSDIST function to approximate the area under the curve.

For example, if we have a normal distribution curve with mean μ = 0 and standard deviation σ = 1, and we want to find the area under the curve from x = -1 to x = 1, we can use the NORMSDIST function as follows:

=NORMSDIST(1) - NORMSDIST(-1)

This will return the approximate area under the curve.

Steps to Use the NORMSDIST Function

• Define the function (e.g., normal distribution with μ = 0 and σ = 1).
• Specify the limits of integration (e.g., x = -1 and x = 1).
• Use the NORMSDIST function (e.g., =NORMSDIST(1) - NORMSDIST(-1)).

Excel Functions for Area Under Curve Image Gallery

In conclusion, finding the area under a curve in Excel can be achieved using various methods, including the SUM function, the INT function, and numerical integration using the NORMSDIST function. The choice of method depends on the complexity of the curve and the desired level of accuracy.

If you have any questions or need further clarification on any of these methods, please don't hesitate to ask in the comments section below.