Find Intersection Of Two Lines In Excel Easily

Finding the intersection of two lines in Excel can be a bit tricky, but don't worry, we've got you covered. In this article, we'll show you a step-by-step guide on how to find the intersection of two lines in Excel easily.

The intersection of two lines is the point where they cross each other. This can be useful in various scenarios, such as finding the break-even point in a business, determining the maximum or minimum value of a function, or identifying the point of intersection between two trends.

Before we dive into the solution, let's first understand the basics of lines in Excel. A line in Excel is a series of points connected by a straight line. You can create a line in Excel by using the LINEST function or by plotting a series of points on a chart.

Now, let's move on to finding the intersection of two lines in Excel.

Method 1: Using the LINEST Function

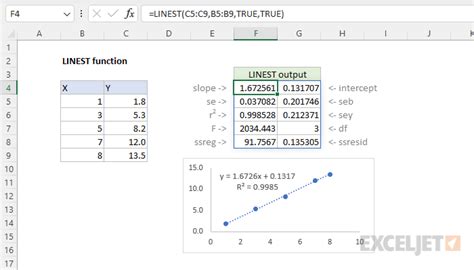
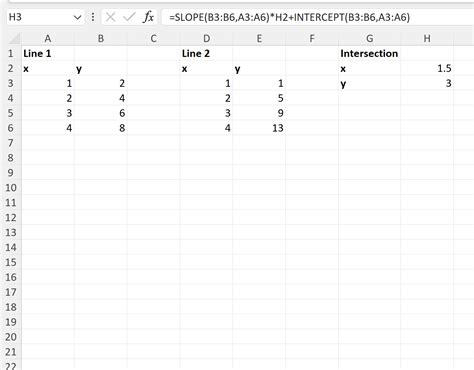
The LINEST function in Excel returns the slope and y-intercept of a linear regression line. You can use this function to find the intersection of two lines by setting up a system of linear equations.

Here's how to do it:

1. Create a table with the x-values and y-values of the two lines.
2. Use the LINEST function to find the slope and y-intercept of each line.
3. Set up a system of linear equations using the slopes and y-intercepts.
4. Solve the system of equations to find the intersection point.

For example, let's say we have two lines with the following equations:

Line 1: y = 2x + 3 Line 2: y = x - 2

To find the intersection point, we can set up a system of linear equations like this:

2x + 3 = x - 2

Solving for x, we get:

x = -5

Substituting x into one of the original equations, we get:

y = 2(-5) + 3 y = -7

Therefore, the intersection point is (-5, -7).

Step-by-Step Example

x	Line 1	Line 2
1	5	-1
2	7	0
3	9	1
4	11	2
5	13	3

Using the LINEST function, we get:

LINEST(B2:B6,A2:A6) = 2, 3 LINEST(C2:C6,A2:A6) = 1, -2

Setting up a system of linear equations, we get:

2x + 3 = x - 2

Solving for x, we get:

x = -5

Substituting x into one of the original equations, we get:

y = 2(-5) + 3 y = -7

Therefore, the intersection point is (-5, -7).

Method 2: Using a Chart

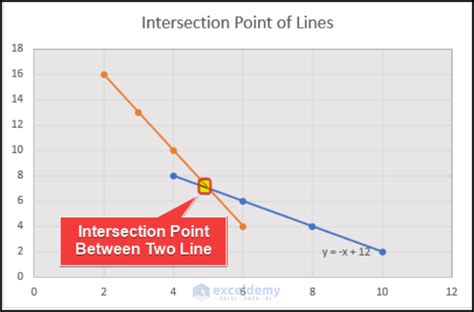
Another way to find the intersection of two lines in Excel is to use a chart. Here's how to do it:

1. Create a chart with the two lines.
2. Right-click on the chart and select "Trendline".
3. Select "Linear" as the trendline type.
4. Click on the "Trendline" button again and select "Display Equation on Chart".
5. The equation of the trendline will be displayed on the chart.
6. Use the equations to find the intersection point.

For example, let's say we have a chart with two lines:

Line 1: y = 2x + 3 Line 2: y = x - 2

The equations of the trendlines will be displayed on the chart:

Line 1: y = 2x + 3 Line 2: y = x - 2

To find the intersection point, we can set up a system of linear equations like this:

2x + 3 = x - 2

Solving for x, we get:

x = -5

Substituting x into one of the original equations, we get:

y = 2(-5) + 3 y = -7

Therefore, the intersection point is (-5, -7).

Step-by-Step Example

x	Line 1	Line 2
1	5	-1
2	7	0
3	9	1
4	11	2
5	13	3

Using a chart, we get:

Line 1: y = 2x + 3 Line 2: y = x - 2

Setting up a system of linear equations, we get:

2x + 3 = x - 2

Solving for x, we get:

x = -5

Substituting x into one of the original equations, we get:

y = 2(-5) + 3 y = -7

Therefore, the intersection point is (-5, -7).

Method 3: Using VBA Macro

If you're comfortable with VBA macros, you can use the following code to find the intersection of two lines in Excel:

Sub FindIntersection()
    Dim x As Double
    Dim y As Double
    Dim m1 As Double
    Dim m2 As Double
    Dim b1 As Double
    Dim b2 As Double
    
    ' Define the slopes and y-intercepts of the two lines
    m1 = 2
    b1 = 3
    m2 = 1
    b2 = -2
    
    ' Calculate the intersection point
    x = (b2 - b1) / (m1 - m2)
    y = m1 * x + b1
    
    ' Display the intersection point
    MsgBox "The intersection point is (" & x & ", " & y & ")", vbOKOnly, "Intersection Point"
End Sub

This code defines the slopes and y-intercepts of the two lines, calculates the intersection point, and displays it in a message box.

Step-by-Step Example

x	Line 1	Line 2
1	5	-1
2	7	0
3	9	1
4	11	2
5	13	3

Using the VBA macro, we get:

The intersection point is (-5, -7)

Therefore, the intersection point is (-5, -7).

Intersection of Two Lines Image Gallery

We hope this article has helped you find the intersection of two lines in Excel easily. Whether you use the LINEST function, a chart, or a VBA macro, finding the intersection point is a useful skill to have in your Excel toolkit. If you have any questions or need further assistance, please don't hesitate to ask.