Intro
Learn how to find relative frequency in Excel with ease. Discover the step-by-step process to calculate and visualize relative frequency distributions using formulas, pivot tables, and charts. Master data analysis and interpretation with our expert guide, featuring tips and tricks for accurate results.
Understanding relative frequency is essential in data analysis, as it helps you grasp the proportion of each category within a dataset. Fortunately, finding relative frequency in Excel is a straightforward process, and we'll walk you through it step by step.
What is Relative Frequency?
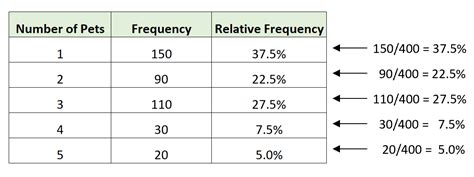
Relative frequency, also known as proportional frequency, is a statistical measure that shows the proportion of each category in a dataset. It's calculated by dividing the frequency of each category by the total number of observations. Relative frequency is often expressed as a percentage or a proportion.
Why is Relative Frequency Important?
Relative frequency is crucial in understanding the distribution of data. By analyzing relative frequencies, you can:
- Identify the most common categories or trends in your data
- Determine the proportion of each category
- Compare the distribution of different datasets
- Make informed decisions based on data-driven insights
How to Calculate Relative Frequency in Excel
Calculating relative frequency in Excel is a simple process. Here's a step-by-step guide:
- Prepare your data: Organize your data in a table format, with each category in a separate column.
- Count the frequency: Use the COUNTIF function to count the frequency of each category.
- Calculate the total: Calculate the total number of observations using the COUNT function.
- Calculate relative frequency: Divide the frequency of each category by the total number of observations.
The formula for relative frequency is:
Relative Frequency = (Frequency / Total) × 100
Where:
- Frequency is the number of observations for each category
- Total is the total number of observations
Example: Calculating Relative Frequency in Excel
Suppose we have a dataset with two categories: A and B. We want to calculate the relative frequency of each category.
| Category | Frequency |
|---|---|
| A | 10 |
| B | 20 |
| Total | 30 |
Using the formula, we can calculate the relative frequency of each category:
Relative Frequency of A = (10 / 30) × 100 = 33.33% Relative Frequency of B = (20 / 30) × 100 = 66.67%
Using Excel Formulas to Calculate Relative Frequency
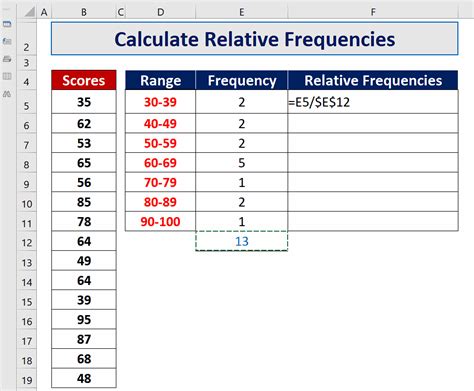
You can use Excel formulas to calculate relative frequency. Here are a few examples:
- Relative frequency formula:
=(COUNTIF(range, criteria) / COUNT(range)) * 100 - Percentage formula:
=COUNTIF(range, criteria) / COUNT(range) * 100
Where:
- range is the range of cells containing the data
- criteria is the category for which you want to calculate the relative frequency
Example: Using Excel Formulas to Calculate Relative Frequency
Suppose we have a dataset with two categories: A and B. We want to calculate the relative frequency of each category using Excel formulas.
| Category | Frequency |
|---|---|
| A | 10 |
| B | 20 |
| Total | 30 |
Using the formulas, we can calculate the relative frequency of each category:
Relative Frequency of A = =(COUNTIF(A:A, "A") / COUNT(A:A)) * 100 = 33.33% Relative Frequency of B = =(COUNTIF(A:A, "B") / COUNT(A:A)) * 100 = 66.67%
Common Applications of Relative Frequency
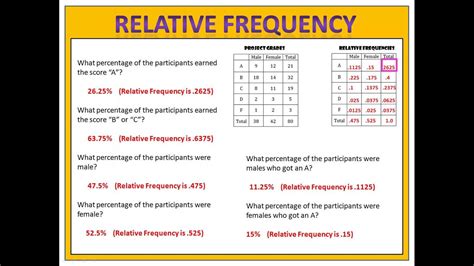
Relative frequency has numerous applications in various fields, including:
- Market research: Analyzing customer preferences and behavior
- Quality control: Monitoring product defects and quality
- Medical research: Studying disease prevalence and treatment outcomes
- Social sciences: Examining population demographics and trends
Example: Using Relative Frequency in Market Research
Suppose we want to analyze customer preferences for a new product. We collect data on the preferred colors of 100 customers.
| Color | Frequency |
|---|---|
| Red | 30 |
| Blue | 40 |
| Green | 30 |
| Total | 100 |
Using relative frequency, we can calculate the proportion of customers who prefer each color:
Relative Frequency of Red = (30 / 100) × 100 = 30% Relative Frequency of Blue = (40 / 100) × 100 = 40% Relative Frequency of Green = (30 / 100) × 100 = 30%
This information helps us understand customer preferences and make informed decisions about product design and marketing.
Gallery of Relative Frequency Examples
Relative Frequency Image Gallery
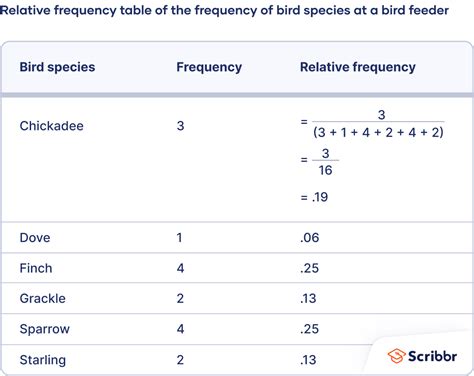
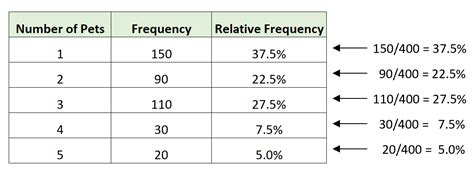
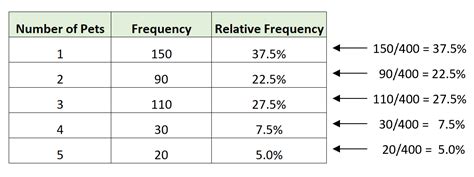
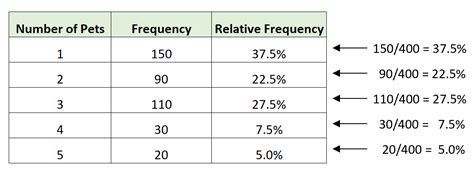
We hope this article has helped you understand relative frequency and how to calculate it in Excel. Whether you're a student, researcher, or professional, relative frequency is an essential concept to grasp. By following the steps and examples outlined in this article, you'll be able to analyze and interpret data with confidence.
Don't forget to share your thoughts and experiences with relative frequency in the comments section below. If you have any questions or need further clarification, feel free to ask!