Integrating Inverse Trig Functions

Inverse trig functions are a crucial part of calculus and are used to solve a wide range of problems in mathematics, physics, and engineering. The inverse trig functions, also known as arcus functions, are the inverse of the trigonometric functions sine, cosine, and tangent. In this article, we will explore the importance of inverse trig functions, their properties, and how they are used in integration.

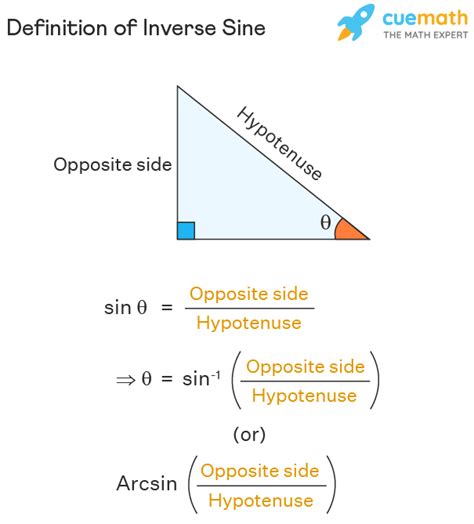
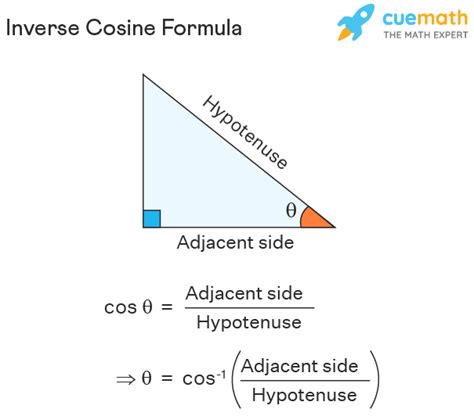
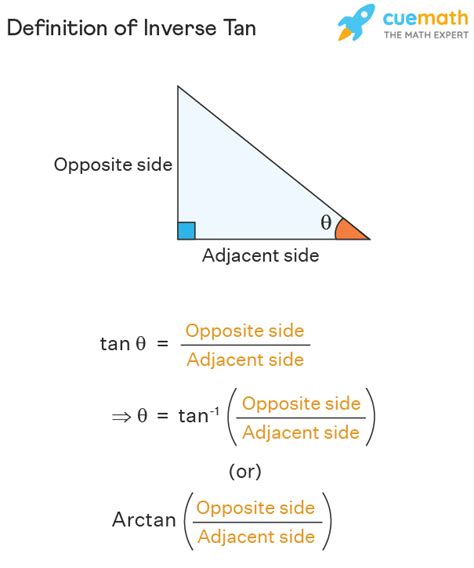
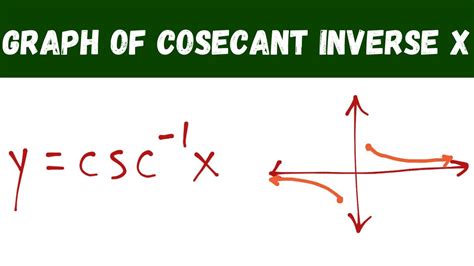
Inverse trig functions are used to find the angle whose trigonometric function is a given value. For example, the inverse sine function, denoted as sin^-1(x), gives the angle whose sine is x. Similarly, the inverse cosine function, denoted as cos^-1(x), gives the angle whose cosine is x. The inverse tangent function, denoted as tan^-1(x), gives the angle whose tangent is x.

The inverse trig functions have several important properties that make them useful in integration. One of the most important properties is that they are odd functions, meaning that sin^-1(-x) = -sin^-1(x), cos^-1(-x) = -cos^-1(x), and tan^-1(-x) = -tan^-1(x). This property makes it easy to integrate inverse trig functions.

Another important property of inverse trig functions is that they have a range of values that they can take. For example, the range of sin^-1(x) is [-π/2, π/2], the range of cos^-1(x) is [0, π], and the range of tan^-1(x) is (-π/2, π/2). This range of values is important to consider when integrating inverse trig functions.

Introduction to Inverse Trig Functions

Inverse trig functions are used in a wide range of applications, including physics, engineering, and mathematics. They are used to solve problems involving right triangles, such as finding the length of a side or the measure of an angle. They are also used in more advanced applications, such as solving differential equations and integrating functions.

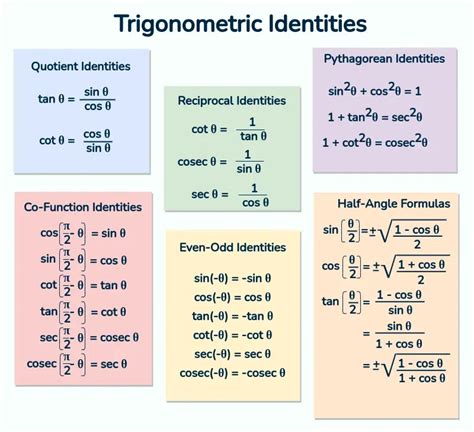
Properties of Inverse Trig Functions

The properties of inverse trig functions are important to understand in order to use them effectively in integration. Some of the key properties include:

The inverse sine function, sin^-1(x), is an odd function, meaning that sin^-1(-x) = -sin^-1(x).
The inverse cosine function, cos^-1(x), is an even function, meaning that cos^-1(-x) = cos^-1(x).
The inverse tangent function, tan^-1(x), is an odd function, meaning that tan^-1(-x) = -tan^-1(x).
The range of sin^-1(x) is [-π/2, π/2].
The range of cos^-1(x) is [0, π].
The range of tan^-1(x) is (-π/2, π/2).

Integration of Inverse Trig Functions

The integration of inverse trig functions is an important application of these functions. The integration of inverse trig functions can be used to solve a wide range of problems, including finding the area under a curve and solving differential equations.

Some of the key formulas for integrating inverse trig functions include:

∫sin^-1(x) dx = x sin^-1(x) + √(1-x^2) + C
∫cos^-1(x) dx = x cos^-1(x) - √(1-x^2) + C
∫tan^-1(x) dx = x tan^-1(x) - (1/2) ln(1+x^2) + C

These formulas can be used to integrate a wide range of functions that involve inverse trig functions.

Applications of Inverse Trig Functions

Inverse trig functions have a wide range of applications in physics, engineering, and mathematics. Some of the key applications include:

Solving problems involving right triangles, such as finding the length of a side or the measure of an angle.
Solving differential equations, such as the equation of motion for an object under the influence of a force.
Integrating functions, such as finding the area under a curve.
Solving problems in physics, such as finding the trajectory of a projectile or the vibration of a spring.

Examples of Inverse Trig Functions

Here are some examples of inverse trig functions:

Find the value of sin^-1(1/2).
Find the value of cos^-1(-1/2).
Find the value of tan^-1(1).
Find the integral of sin^-1(x) from 0 to 1.
Find the integral of cos^-1(x) from -1 to 1.

These examples illustrate the use of inverse trig functions in a wide range of applications.

Gallery of Inverse Trig Functions

Inverse Trig Functions Image Gallery

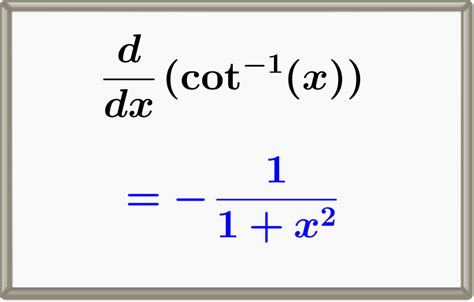
Frequently Asked Questions

Here are some frequently asked questions about inverse trig functions:

What is the range of sin^-1(x)?
What is the range of cos^-1(x)?
What is the range of tan^-1(x)?
How do I integrate sin^-1(x)?
How do I integrate cos^-1(x)?
How do I integrate tan^-1(x)?

These questions illustrate the common confusion and misunderstandings about inverse trig functions.

We hope this article has provided a comprehensive overview of inverse trig functions and their applications. Whether you are a student, teacher, or professional, understanding inverse trig functions is essential for success in mathematics, physics, and engineering. We invite you to comment, share this article, or ask questions about inverse trig functions. With practice and patience, you can master inverse trig functions and apply them to solve a wide range of problems.