Inverting a matrix is a fundamental concept in linear algebra and is used extensively in various fields, including engineering, economics, and computer science. In Microsoft Excel, inverting a matrix can be a bit tricky, but with the right techniques, it can be done easily and quickly.
Understanding Matrix Inversion

Before we dive into the process of inverting a matrix in Excel, it's essential to understand what matrix inversion is and why it's useful. Matrix inversion is the process of finding the inverse of a square matrix, which is a matrix with the same number of rows and columns. The inverse of a matrix A, denoted by A^(-1), is a matrix that, when multiplied by A, results in the identity matrix I.
Why Invert a Matrix?
Inverting a matrix is useful in various applications, including:
- Solving systems of linear equations
- Finding the determinant of a matrix
- Calculating the eigenvalues and eigenvectors of a matrix
- Performing linear transformations
Methods for Inverting a Matrix in Excel
There are several methods for inverting a matrix in Excel, including:
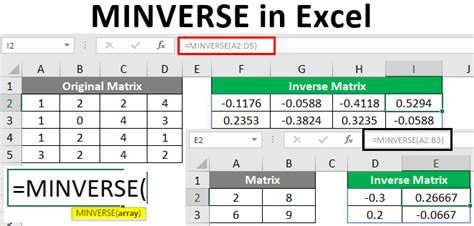
Method 1: Using the MINVERSE Function
The MINVERSE function is a built-in function in Excel that calculates the inverse of a matrix. To use this function, follow these steps:
- Select the cell range where you want to display the inverted matrix.
- Type "=MINVERSE(" and select the cell range that contains the matrix you want to invert.
- Close the parenthesis and press Enter.
For example, if the matrix you want to invert is in the cell range A1:C3, the formula would be:
=MINVERSE(A1:C3)
Method 2: Using the Solver Add-in
The Solver add-in is a powerful tool in Excel that can be used to invert a matrix. To use the Solver add-in, follow these steps:
- Select the cell range where you want to display the inverted matrix.
- Go to the Data tab in the ribbon and click on the Solver button.
- In the Solver Parameters dialog box, select the cell range that contains the matrix you want to invert.
- Click on the Options button and select the "Inverse" option.
- Click OK to calculate the inverse of the matrix.
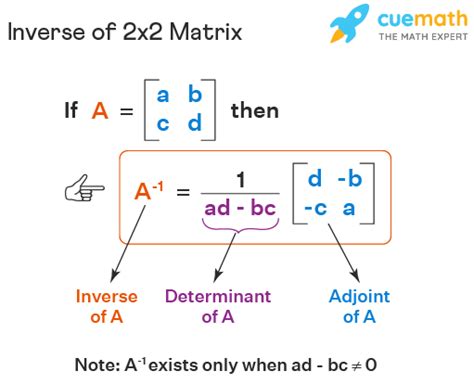
Method 3: Using the Matrix Inversion Formula
If you don't have access to the MINVERSE function or the Solver add-in, you can use the matrix inversion formula to invert a matrix. The formula is:
A^(-1) = 1/det(A) * adj(A)
where det(A) is the determinant of the matrix A, and adj(A) is the adjugate of the matrix A.
To use this formula in Excel, follow these steps:
- Calculate the determinant of the matrix using the formula: det(A) = A11*A22 - A12*A21
- Calculate the adjugate of the matrix using the formula: adj(A) = [A11, A12; A21, A22]
- Calculate the inverse of the matrix using the formula: A^(-1) = 1/det(A) * adj(A)
Examples and Applications
Inverting a matrix has numerous applications in various fields. Here are a few examples:
- Solving a system of linear equations:
Suppose we have a system of linear equations:
2x + 3y = 7 x - 2y = -3
We can represent this system as a matrix equation:
| 2 3 | | x | | 7 | | x -2 | | y | = | -3|
To solve this system, we can invert the matrix and multiply it by the constant matrix:
| 2 3 |^(-1) * | 7 | | x -2 | | -3|
Using the MINVERSE function, we can calculate the inverse of the matrix and solve the system:
=MINVERSE(A1:C2) * D1:E2
- Finding the determinant of a matrix:
The determinant of a matrix can be used to determine the solvability of a system of linear equations. To calculate the determinant of a matrix, we can use the formula:
det(A) = A11*A22 - A12*A21
For example, if the matrix is:
| 2 3 | | x -2 |
The determinant is:
det(A) = 2* (-2) - 3*x = -4 - 3x
Gallery of Matrix Inversion Techniques
Matrix Inversion Techniques Image Gallery






Conclusion and Next Steps
Inverting a matrix is a fundamental concept in linear algebra and has numerous applications in various fields. In this article, we have discussed three methods for inverting a matrix in Excel, including using the MINVERSE function, the Solver add-in, and the matrix inversion formula. We have also provided examples and applications of matrix inversion.
If you have any questions or need further assistance, please don't hesitate to ask. You can also share your own experiences and tips for inverting matrices in Excel in the comments section below.
Remember to practice and apply your knowledge of matrix inversion to solve real-world problems and improve your skills in linear algebra.
