Intro
Master linear interpolation with our 5-step formula guide. Learn to calculate unknown values easily and accurately between two known data points. Discover how to apply this mathematical technique in various fields, including science, engineering, and finance, using linear interpolation methods and nearest neighbor interpolation.
Are you tired of tedious calculations when working with data sets that require interpolations? Look no further! Linear interpolation is a powerful tool that can help you estimate unknown values between two known data points. In this article, we will explore the 5-step linear interpolation formula guide, making it easier for you to calculate values with precision.

Linear interpolation is a widely used technique in various fields, including mathematics, physics, engineering, and computer science. It is particularly useful when dealing with large data sets or when you need to estimate values between two known data points. By following the 5-step linear interpolation formula guide, you'll be able to calculate values easily and accurately.
What is Linear Interpolation?
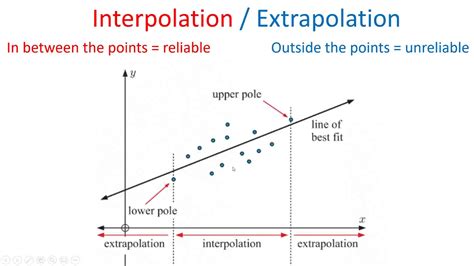
Linear interpolation is a method of estimating a value between two known data points by creating a linear equation that connects the two points. The equation is used to calculate the unknown value based on the proportional distance between the two known points. This technique is particularly useful when working with data sets that have a linear relationship between the variables.
Why Use Linear Interpolation?
There are several reasons why linear interpolation is a popular technique:
- It's simple and easy to use.
- It's fast and efficient, even with large data sets.
- It provides accurate results, especially when the data points are close together.
- It's widely used in various fields, making it a versatile technique.
5-Step Linear Interpolation Formula Guide
Now that we've covered the basics of linear interpolation, let's dive into the 5-step formula guide. Follow these steps to calculate values easily:

Step 1: Identify the Known Data Points
Identify the two known data points that you want to use for interpolation. These points should have a linear relationship between the variables.
Step 2: Determine the Unknown Value
Determine the unknown value that you want to estimate. This value should be within the range of the two known data points.
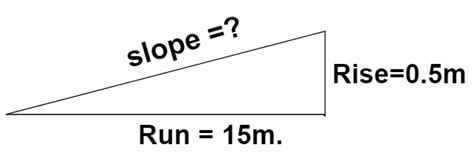
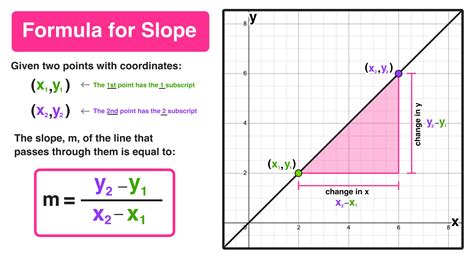
Step 3: Calculate the Slope
Calculate the slope of the line that connects the two known data points. The slope is calculated using the formula:
m = (y2 - y1) / (x2 - x1)
where m is the slope, and (x1, y1) and (x2, y2) are the known data points.
Step 4: Calculate the Linear Equation
Calculate the linear equation that connects the two known data points using the slope and one of the data points. The equation is in the form:
y = mx + b
where y is the unknown value, m is the slope, x is the independent variable, and b is the y-intercept.
Step 5: Calculate the Unknown Value
Calculate the unknown value using the linear equation and the independent variable. Simply plug in the value of x into the equation and solve for y.
Example of Linear Interpolation
Let's consider an example to illustrate the 5-step linear interpolation formula guide. Suppose we have two known data points:
| x | y |
|---|---|
| 2 | 4 |
| 6 | 8 |
We want to estimate the value of y when x is 4.

Using the 5-step formula guide, we can calculate the slope, linear equation, and unknown value.
Step 1: Identify the Known Data Points
The known data points are (2, 4) and (6, 8).
Step 2: Determine the Unknown Value
We want to estimate the value of y when x is 4.
Step 3: Calculate the Slope
The slope is calculated using the formula:
m = (8 - 4) / (6 - 2) m = 4 / 4 m = 1
Step 4: Calculate the Linear Equation
The linear equation is calculated using the slope and one of the data points:
y = mx + b y = 1x + b Using the data point (2, 4), we can solve for b: 4 = 1(2) + b b = 2
The linear equation is:
y = x + 2
Step 5: Calculate the Unknown Value
We can calculate the unknown value using the linear equation and the independent variable:
y = x + 2 y = 4 + 2 y = 6
Therefore, the estimated value of y when x is 4 is 6.
Gallery of Linear Interpolation
Linear Interpolation Image Gallery




Conclusion
Linear interpolation is a powerful tool for estimating unknown values between two known data points. By following the 5-step linear interpolation formula guide, you can calculate values easily and accurately. Remember to identify the known data points, determine the unknown value, calculate the slope, calculate the linear equation, and calculate the unknown value. With practice, you'll become proficient in using linear interpolation to solve problems in various fields.
We hope this article has been informative and helpful. If you have any questions or comments, please feel free to share them below. Don't forget to share this article with your friends and colleagues who may benefit from learning about linear interpolation.
What are your thoughts on linear interpolation? Have you used this technique in your work or studies? Share your experiences and insights in the comments section below.
