Mann Whitney Test In Excel Made Easy

The Mann-Whitney test, also known as the Wilcoxon rank-sum test, is a non-parametric statistical test used to compare the distributions of two independent samples. It's a powerful tool for determining whether there's a significant difference between two groups. In this article, we'll explore how to perform a Mann-Whitney test in Excel, making it easy to understand and apply to your data analysis needs.

Why Use the Mann-Whitney Test?

The Mann-Whitney test is a versatile and widely used statistical test that offers several advantages. It's particularly useful when:

• The data is not normally distributed
• The sample sizes are small
• The data is ordinal or ranked
• You want to compare the distributions of two independent samples

Assumptions of the Mann-Whitney Test

Before performing the Mann-Whitney test, ensure that your data meets the following assumptions:

• The data is independent and identically distributed (i.i.d.)
• The data is ordinal or ranked
• There are no ties or zero differences between the data points

How to Perform a Mann-Whitney Test in Excel

Performing a Mann-Whitney test in Excel is relatively straightforward. Here's a step-by-step guide:

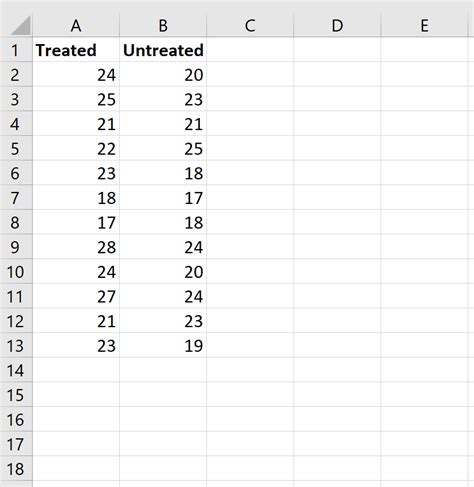
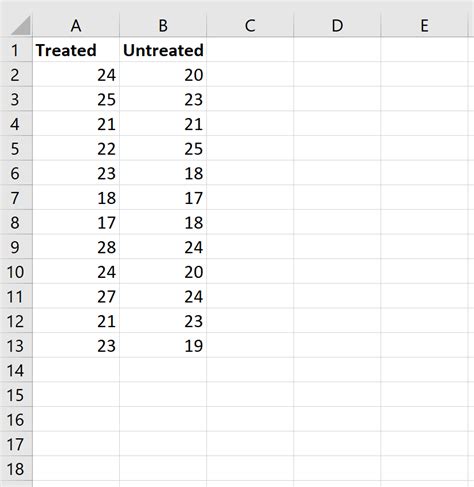
Step 1: Prepare Your Data

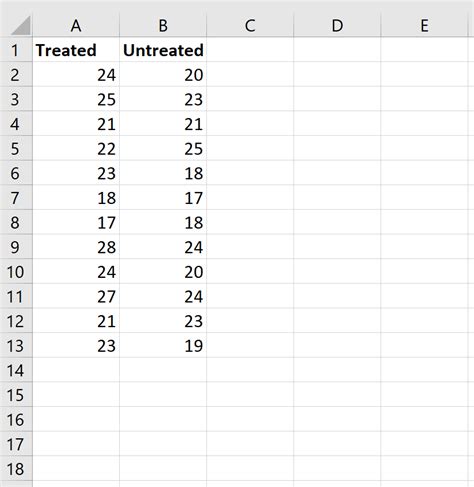
Ensure your data is organized in two separate columns, with each column representing a different group or sample.

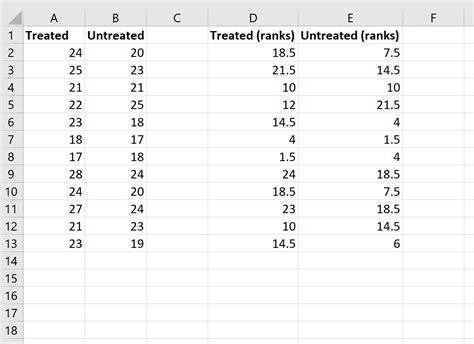
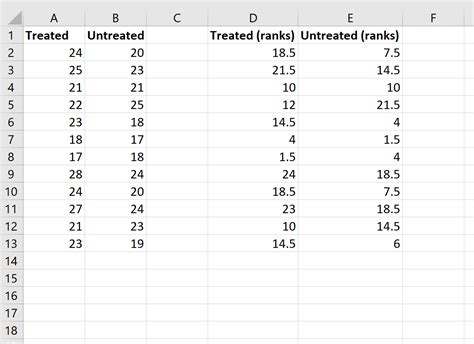
Step 2: Calculate the Ranks

Calculate the ranks for each data point using the RANK function in Excel. This will help you to determine the relative position of each data point within its respective group.

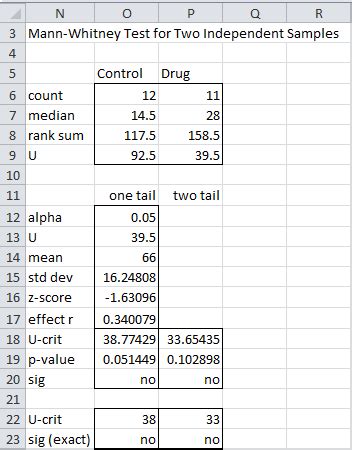
Step 3: Calculate the Test Statistic

Calculate the test statistic (U) using the following formula:

U = n1 * n2 + (n1 * (n1 + 1)) / 2 - ∑(Ri)

where n1 and n2 are the sample sizes, and Ri is the rank of each data point.

Step 4: Calculate the P-Value

Calculate the p-value using the NORMSDIST function in Excel. This will give you the probability of observing a test statistic at least as extreme as the one you calculated.

Step 5: Interpret the Results

Compare the p-value to your chosen significance level (usually 0.05). If the p-value is less than the significance level, you can reject the null hypothesis and conclude that there's a significant difference between the two groups.

Mann-Whitney Test Excel Formula

If you prefer to use a formula instead of the steps outlined above, you can use the following formula:

=MANNWHITNEY(U, n1, n2)

where U is the test statistic, and n1 and n2 are the sample sizes.

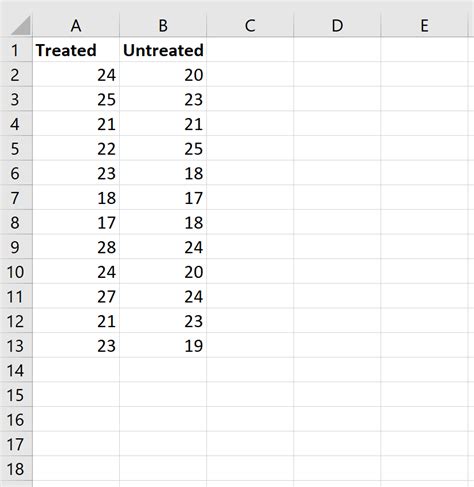
Example

Suppose you want to compare the exam scores of two groups of students. Group A consists of 10 students with scores: 85, 90, 78, 92, 88, 76, 95, 89, 91, 84. Group B consists of 12 students with scores: 80, 85, 70, 90, 88, 76, 92, 89, 91, 84, 82, 86.

To perform the Mann-Whitney test, follow the steps outlined above. Calculate the ranks, test statistic, and p-value. Compare the p-value to your chosen significance level and interpret the results.

Common Mistakes to Avoid

When performing a Mann-Whitney test in Excel, be sure to avoid the following common mistakes:

• Failing to check the assumptions of the test
• Incorrectly calculating the ranks or test statistic
• Misinterpreting the p-value or results

Conclusion

The Mann-Whitney test is a powerful statistical tool for comparing the distributions of two independent samples. By following the steps outlined in this article, you can easily perform a Mann-Whitney test in Excel and gain valuable insights into your data.

Mann-Whitney Test Excel Gallery

Share Your Thoughts

We hope this article has helped you understand how to perform a Mann-Whitney test in Excel. Share your thoughts and experiences with us in the comments below. Have you used the Mann-Whitney test in your research or data analysis? What challenges did you face, and how did you overcome them?