Mann Whitney U Test In Excel Made Easy

The Mann Whitney U test is a non-parametric statistical test used to compare the distributions of two independent samples. It's a powerful tool for analyzing data, but can be intimidating to use, especially for those without a strong statistical background. Fortunately, Excel provides a relatively easy way to perform the Mann Whitney U test, and in this article, we'll guide you through the process.

What is the Mann Whitney U Test?

The Mann Whitney U test is a non-parametric alternative to the t-test, used to compare the means of two independent samples. It's commonly used when the data doesn't meet the assumptions of the t-test, such as normality or equal variances. The test is also useful when the data is ordinal or ranked.

How the Mann Whitney U Test Works

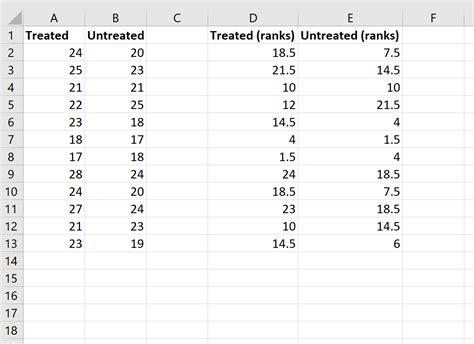
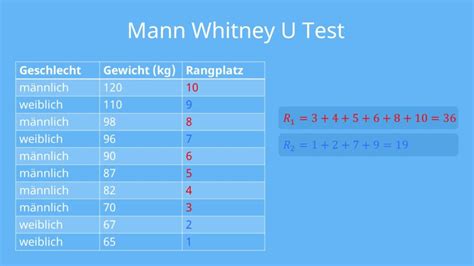
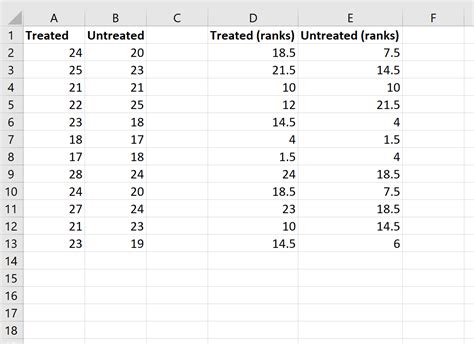
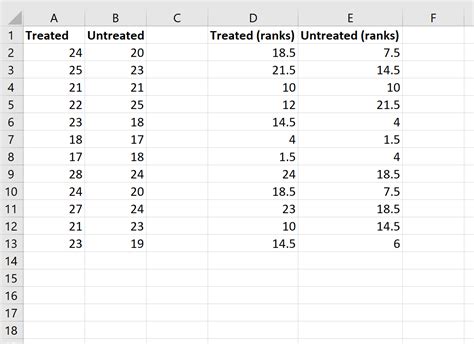
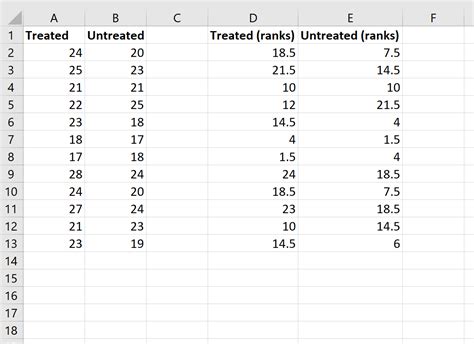
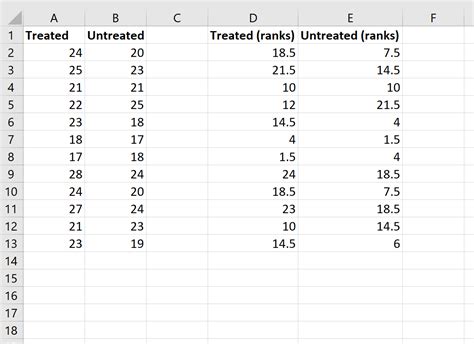
The Mann Whitney U test works by combining the two samples into a single dataset and ranking the values from smallest to largest. The test then calculates the number of times a value from one sample is ranked higher than a value from the other sample. This is known as the U statistic.

The U statistic is then compared to a critical value from a standard normal distribution, or a p-value is calculated to determine the significance of the result.

Performing the Mann Whitney U Test in Excel

To perform the Mann Whitney U test in Excel, you'll need to use the Analysis ToolPak add-in. Here's a step-by-step guide:

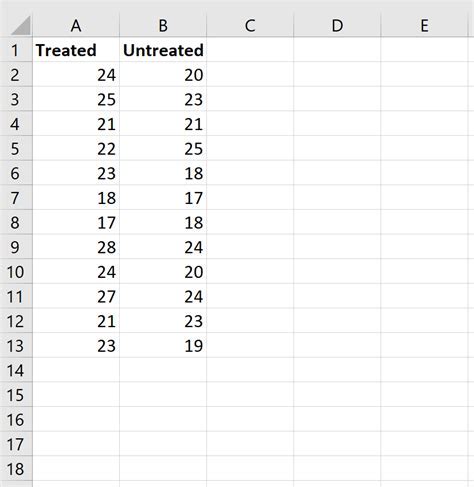
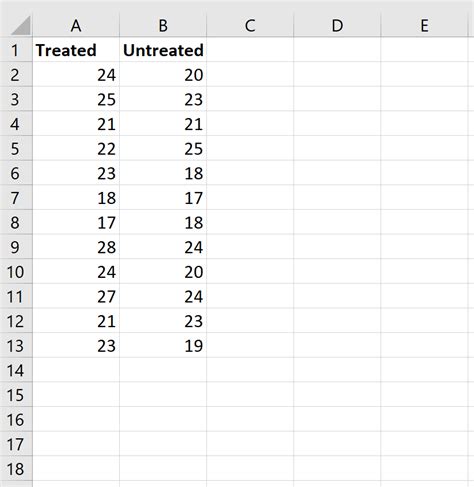
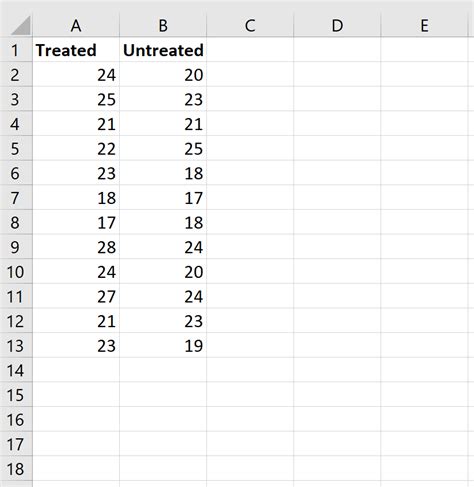
Select the data range for the two samples, including headers.
Go to the "Data" tab and click on "Data Analysis".
Select "Nonparametric Tests" and click "OK".
Select "2-Samples" and click "OK".
Choose the test type as "Mann-Whitney U".
Select the sample ranges and click "OK".

Interpreting the Results

The results of the Mann Whitney U test will include the U statistic, the p-value, and the critical region.

The U statistic represents the number of times a value from one sample is ranked higher than a value from the other sample.
The p-value represents the probability of observing the U statistic (or a more extreme value) assuming that the two samples come from the same distribution.
The critical region represents the range of values for the U statistic that would lead to rejection of the null hypothesis.

If the p-value is less than the chosen significance level (e.g., 0.05), you can reject the null hypothesis and conclude that the two samples come from different distributions.

Common Applications of the Mann Whitney U Test

The Mann Whitney U test has a wide range of applications in various fields, including:

Medical research: to compare the outcomes of two treatments
Marketing research: to compare the preferences of two groups of consumers
Quality control: to compare the quality of two products
Social sciences: to compare the attitudes or behaviors of two groups

Limitations of the Mann Whitney U Test

While the Mann Whitney U test is a powerful tool, it has some limitations:

The test assumes that the data is independent and identically distributed.
The test is sensitive to outliers and skewness.
The test is not suitable for paired or matched data.

Alternatives to the Mann Whitney U Test

If the assumptions of the Mann Whitney U test are not met, or if the data is paired or matched, alternative tests can be used, such as:

Wilcoxon rank-sum test
Wilcoxon signed-rank test
Kolmogorov-Smirnov test

Conclusion

The Mann Whitney U test is a useful non-parametric test for comparing the distributions of two independent samples. With the help of Excel's Analysis ToolPak add-in, performing the test is relatively easy. By understanding the assumptions, applications, and limitations of the test, you can use it to gain insights into your data and make informed decisions.

Mann Whitney U Test Image Gallery

We hope you found this article helpful in understanding the Mann Whitney U test and how to perform it in Excel. If you have any questions or need further clarification, please don't hesitate to ask in the comments below.