Intro
Calculating the margin of error is a crucial step in understanding the reliability of survey results, statistical analyses, or any other data-driven research. In this article, we will explore five ways to calculate the margin of error in Excel, a widely used spreadsheet software. Understanding these methods will help you make informed decisions based on your data analysis.
What is Margin of Error?
Margin of error, also known as the confidence interval, is a statistical measure that represents the amount of random sampling error in a survey or study. It is the maximum amount by which the sample results may differ from the true population value. In simpler terms, it is the plus-or-minus percentage that indicates the reliability of your survey results.
Method 1: Using the Confidence Interval Formula
The most common method of calculating the margin of error is by using the confidence interval formula:
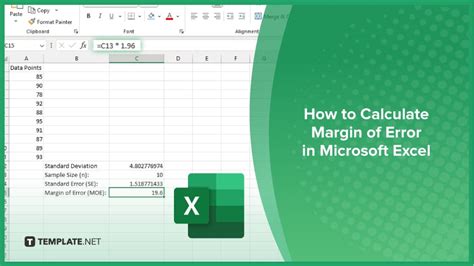
Margin of Error (ME) = (Z * σ) / √n
Where:
- Z = Z-score corresponding to the desired confidence level
- σ = Standard deviation of the population
- n = Sample size
To calculate the margin of error in Excel, follow these steps:
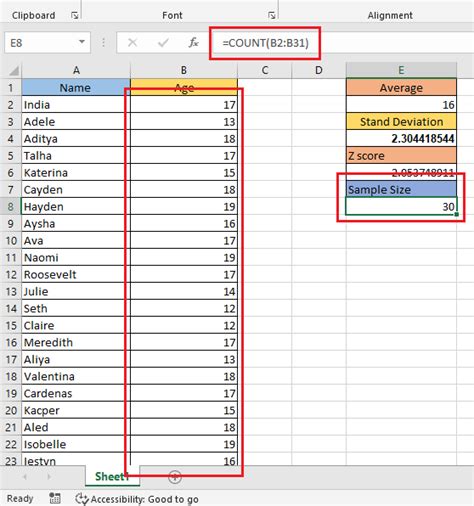
- Calculate the standard deviation (σ) of your data using the STDEV function.
- Determine the Z-score corresponding to your desired confidence level (e.g., 95% confidence level, Z = 1.96).
- Enter the formula
=(Z*σ)/SQRT(n)in an Excel cell, replacing Z, σ, and n with your values.
Example:
Suppose we want to calculate the margin of error for a survey with a sample size of 100, a standard deviation of 10, and a desired confidence level of 95%. The Z-score for a 95% confidence level is 1.96.

Using the formula, we get: ME = (1.96 * 10) / √100 ≈ 1.96
Method 2: Using the Standard Error Formula
Another way to calculate the margin of error is by using the standard error formula:
Margin of Error (ME) = Standard Error (SE) * Z
Where:
- Standard Error (SE) = σ / √n
- Z = Z-score corresponding to the desired confidence level
To calculate the margin of error in Excel, follow these steps:
- Calculate the standard deviation (σ) of your data using the STDEV function.
- Calculate the standard error (SE) using the formula
=σ/SQRT(n). - Determine the Z-score corresponding to your desired confidence level.
- Enter the formula
=SE*Zin an Excel cell, replacing SE and Z with your values.
Example:
Using the same data as before, we calculate the standard error: SE = 10 / √100 ≈ 1
Using the formula, we get: ME = 1 * 1.96 ≈ 1.96
Method 3: Using the Margin of Error Formula with a Proportion
When working with proportions or percentages, you can use a specialized margin of error formula:
Margin of Error (ME) = √(p * (1-p) / n) * Z
Where:
- p = Sample proportion
- n = Sample size
- Z = Z-score corresponding to the desired confidence level
To calculate the margin of error in Excel, follow these steps:
- Calculate the sample proportion (p) using the formula
=COUNTIFS(data range, criteria) / COUNT(data range). - Determine the Z-score corresponding to your desired confidence level.
- Enter the formula
=SQRT(p*(1-p)/n)*Zin an Excel cell, replacing p, n, and Z with your values.
Example:
Suppose we want to calculate the margin of error for a survey with a sample size of 100, a sample proportion of 0.5, and a desired confidence level of 95%. The Z-score for a 95% confidence level is 1.96.

Using the formula, we get: ME = √(0.5 * (1-0.5) / 100) * 1.96 ≈ 0.049
Method 4: Using the CONFIDENCE.NORM Function
Excel provides a built-in function, CONFIDENCE.NORM, which can calculate the margin of error for you:
CONFIDENCE.NORM(alpha, standard_dev, size)
Where:
- alpha = 1 - desired confidence level (e.g., 0.05 for 95% confidence)
- standard_dev = Standard deviation of the population
- size = Sample size
To calculate the margin of error in Excel, follow these steps:
- Determine the desired confidence level and convert it to alpha (e.g., 0.05 for 95% confidence).
- Calculate the standard deviation (σ) of your data using the STDEV function.
- Enter the formula
=CONFIDENCE.NORM(alpha, σ, n)in an Excel cell, replacing alpha, σ, and n with your values.
Example:
Using the same data as before, we calculate the margin of error: CONFIDENCE.NORM(0.05, 10, 100) ≈ 1.96
Method 5: Using the CONFIDENCE.T Function
If you don't know the population standard deviation, you can use the CONFIDENCE.T function, which uses the sample standard deviation instead:
CONFIDENCE.T(alpha, standard_dev, size)
Where:
- alpha = 1 - desired confidence level (e.g., 0.05 for 95% confidence)
- standard_dev = Sample standard deviation
- size = Sample size
To calculate the margin of error in Excel, follow these steps:
- Determine the desired confidence level and convert it to alpha (e.g., 0.05 for 95% confidence).
- Calculate the sample standard deviation (s) of your data using the STDEV.S function.
- Enter the formula
=CONFIDENCE.T(alpha, s, n)in an Excel cell, replacing alpha, s, and n with your values.
Example:
Using the same data as before, we calculate the margin of error: CONFIDENCE.T(0.05, 10, 100) ≈ 1.96
Margin of Error Image Gallery







Now that you have learned the five ways to calculate the margin of error in Excel, it's essential to choose the method that best suits your data analysis needs. Remember to always consider the confidence level, sample size, and population standard deviation when calculating the margin of error.
By understanding and applying these methods, you will be able to make informed decisions based on your data analysis and provide more accurate results.
Do you have any questions about calculating the margin of error in Excel? Share your thoughts in the comments below!
