5 Essential Math Formulas

Mathematics is an essential tool for problem-solving and critical thinking. It is a language that helps us understand and describe the world around us. From simple arithmetic to complex calculus, math formulas are used in various aspects of our lives, including science, engineering, economics, and finance. In this article, we will explore five essential math formulas that every student, professional, and enthusiast should know.

These formulas are fundamental building blocks of mathematics and have numerous applications in real-life situations. Mastering these formulas can help individuals develop a deeper understanding of mathematical concepts and improve their problem-solving skills. Whether you are a student looking to excel in math or a professional seeking to enhance your analytical skills, this article will provide you with a comprehensive overview of the five essential math formulas.

Understanding these formulas can also help individuals appreciate the beauty and complexity of mathematics. Math is not just a subject in school; it is a way of thinking, a language that can be used to describe and analyze the world around us. By learning and applying these formulas, individuals can develop a new perspective on problem-solving and critical thinking.

Introduction to Essential Math Formulas

The five essential math formulas we will discuss in this article are the Pythagorean theorem, the quadratic formula, the formula for the area of a circle, the formula for the volume of a sphere, and the formula for compound interest. These formulas are widely used in various fields, including physics, engineering, economics, and finance.

The Pythagorean Theorem

The Pythagorean theorem is one of the most famous math formulas in history. It states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. The formula is:

a^2 + b^2 = c^2

where a and b are the lengths of the two sides, and c is the length of the hypotenuse.

Applications of the Pythagorean Theorem

The Pythagorean theorem has numerous applications in physics, engineering, and architecture. It is used to calculate distances, heights, and lengths of objects, as well as to determine the stability of structures. For example, architects use the Pythagorean theorem to design buildings and bridges, while physicists use it to calculate the trajectories of projectiles.

The Quadratic Formula

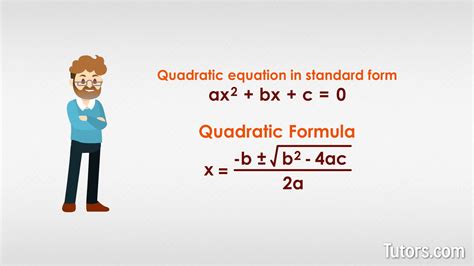
The quadratic formula is a fundamental formula in algebra that is used to solve quadratic equations. A quadratic equation is an equation of the form:

ax^2 + bx + c = 0

where a, b, and c are constants, and x is the variable. The quadratic formula is:

x = (-b ± √(b^2 - 4ac)) / 2a

This formula provides two solutions to the quadratic equation, which can be real or complex numbers.

Applications of the Quadratic Formula

The quadratic formula has numerous applications in physics, engineering, and economics. It is used to model population growth, chemical reactions, and electrical circuits. For example, economists use the quadratic formula to model the behavior of markets and to predict the impact of policy changes.

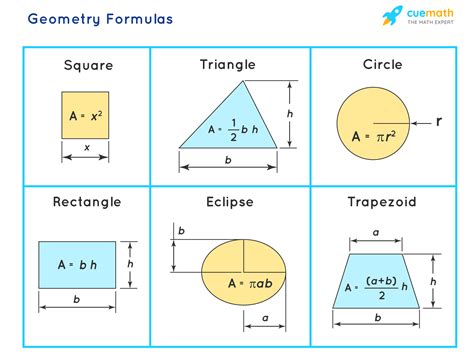
The Formula for the Area of a Circle

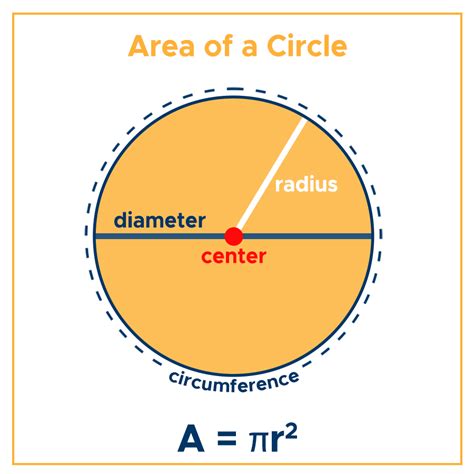
The formula for the area of a circle is a fundamental formula in geometry that is used to calculate the area of a circle. The formula is:

A = πr^2

where A is the area of the circle, and r is the radius of the circle.

Applications of the Formula for the Area of a Circle

The formula for the area of a circle has numerous applications in physics, engineering, and architecture. It is used to calculate the area of circular surfaces, such as pipes, tubes, and cylinders. For example, architects use the formula to design circular buildings and bridges, while physicists use it to calculate the area of circular surfaces in thermal systems.

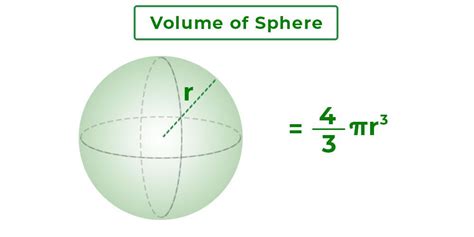
The Formula for the Volume of a Sphere

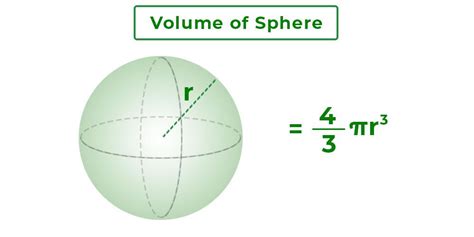
The formula for the volume of a sphere is a fundamental formula in geometry that is used to calculate the volume of a sphere. The formula is:

V = (4/3)πr^3

where V is the volume of the sphere, and r is the radius of the sphere.

Applications of the Formula for the Volume of a Sphere

The formula for the volume of a sphere has numerous applications in physics, engineering, and architecture. It is used to calculate the volume of spherical objects, such as balls, globes, and planets. For example, physicists use the formula to calculate the volume of atoms and molecules, while architects use it to design spherical buildings and bridges.

The Formula for Compound Interest

The formula for compound interest is a fundamental formula in finance that is used to calculate the interest earned on an investment. The formula is:

A = P(1 + r/n)^(nt)

where A is the future value of the investment, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the time in years.

Applications of the Formula for Compound Interest

The formula for compound interest has numerous applications in finance and economics. It is used to calculate the interest earned on savings accounts, investments, and loans. For example, investors use the formula to calculate the returns on their investments, while banks use it to calculate the interest earned on deposits.

Math Formulas Image Gallery

In conclusion, the five essential math formulas discussed in this article are fundamental building blocks of mathematics that have numerous applications in real-life situations. By mastering these formulas, individuals can develop a deeper understanding of mathematical concepts and improve their problem-solving skills. Whether you are a student, professional, or enthusiast, these formulas are essential tools that can help you navigate the world of mathematics and beyond. We invite you to share your thoughts on these formulas and how you have applied them in your own life. Please comment below and share this article with others who may benefit from learning about these essential math formulas.