Calculating the variance-covariance matrix is a crucial step in many statistical analyses, including portfolio optimization, risk management, and regression analysis. While it can be a daunting task, Excel provides an efficient way to calculate the variance-covariance matrix with ease. In this article, we will explore the steps to calculate the variance-covariance matrix in Excel and provide practical examples to illustrate the process.

Understanding the Variance-Covariance Matrix
The variance-covariance matrix is a square matrix that summarizes the variance and covariance between multiple variables. The diagonal elements of the matrix represent the variance of each variable, while the off-diagonal elements represent the covariance between variables. The covariance measures the linear relationship between two variables, and it is an essential concept in understanding the correlation between variables.
Calculating the Variance-Covariance Matrix in Excel
To calculate the variance-covariance matrix in Excel, you can use the COVAR and VAR functions or the Analysis ToolPak add-in. Here, we will demonstrate both methods.
Method 1: Using the COVAR and VAR Functions

Assuming you have a dataset with multiple variables, you can calculate the variance-covariance matrix using the following steps:
- Select the range of cells containing the data.
- Go to the
Formulastab and click onMore Functions>Statistical>COVAR. - Select the range of cells containing the data and click
OK. - The
COVARfunction will return the covariance between the selected variables. - To calculate the variance, use the
VARfunction.
Example
Suppose we have a dataset with two variables, X and Y, and we want to calculate the variance-covariance matrix.
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
Using the COVAR function, we can calculate the covariance between X and Y as follows:
=COVAR(A2:A6,B2:B6)
This will return the covariance between X and Y.
To calculate the variance of X and Y, we can use the VAR function:
=VAR(A2:A6)
=VAR(B2:B6)
These will return the variance of X and Y, respectively.
Method 2: Using the Analysis ToolPak Add-in
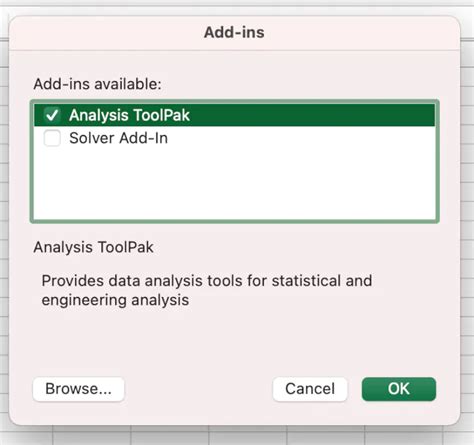
The Analysis ToolPak add-in provides a more efficient way to calculate the variance-covariance matrix. Here's how:
- Go to the
Datatab and click onData Analysis>Analysis ToolPak>Variance-Covariance Matrix. - Select the range of cells containing the data and click
OK. - The Analysis ToolPak will return the variance-covariance matrix.
Example
Using the same dataset as before, we can calculate the variance-covariance matrix using the Analysis ToolPak add-in.
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
The Analysis ToolPak will return the following variance-covariance matrix:
| X | Y | |
|---|---|---|
| X | 2.5 | 3.5 |
| Y | 3.5 | 5.5 |
The diagonal elements represent the variance of X and Y, while the off-diagonal elements represent the covariance between X and Y.
Practical Applications of the Variance-Covariance Matrix
The variance-covariance matrix has numerous practical applications in finance, economics, and engineering. Some of the most common applications include:
- Portfolio optimization: The variance-covariance matrix is used to optimize portfolio returns and minimize risk.
- Risk management: The variance-covariance matrix helps to identify potential risks and correlations between assets.
- Regression analysis: The variance-covariance matrix is used to estimate the variance of regression coefficients.
Variance Covariance Matrix Image Gallery



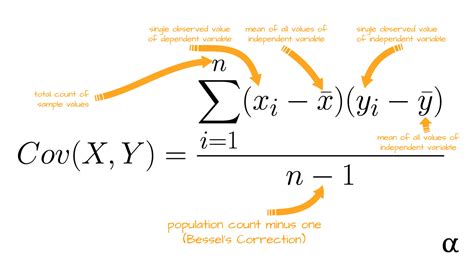
In conclusion, calculating the variance-covariance matrix is a crucial step in many statistical analyses. Excel provides an efficient way to calculate the variance-covariance matrix using the COVAR and VAR functions or the Analysis ToolPak add-in. Understanding the variance-covariance matrix and its applications can help you make informed decisions in finance, economics, and engineering.
We hope this article has been informative and helpful. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences with us in the comments section below.
