Intro
Understanding the Importance of Minimum Detectable Effect
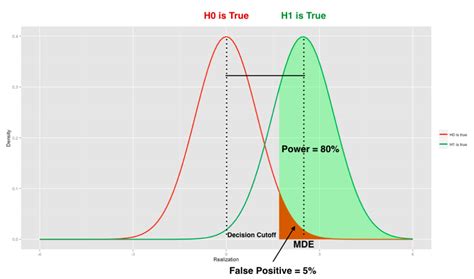
In the realm of statistical analysis and experimental design, understanding the Minimum Detectable Effect (MDE) is crucial for researchers and scientists. The MDE is the smallest effect size that can be detected with a certain level of statistical power, typically set at 80%. In other words, it's the minimum difference between two groups that an experiment can reliably detect. Accurately calculating the MDE is essential to ensure that experiments are designed to detect meaningful effects and to avoid false positives or false negatives. In this article, we'll explore seven ways to calculate the Minimum Detectable Effect and provide practical examples to illustrate each method.
Method 1: Using the Formula for Sample Size Calculation
One common approach to calculate the MDE is to use the formula for sample size calculation. This formula takes into account the desired level of statistical power, the significance level (α), and the effect size (ES). The formula is:
n = (Zα + Zβ)^2 * σ^2 / ES^2
where n is the sample size, Zα is the Z-score corresponding to the desired significance level, Zβ is the Z-score corresponding to the desired power, σ is the standard deviation, and ES is the effect size.
By rearranging this formula, we can solve for the MDE:
MDE = (Zα + Zβ)^2 * σ^2 / n
Example:
Suppose we want to design an experiment to detect a difference in mean blood pressure between two groups with a power of 80% and a significance level of 0.05. Assuming a standard deviation of 10 mmHg and a sample size of 100 participants per group, we can calculate the MDE as follows:
MDE = (1.96 + 0.842)^2 * 10^2 / 100 ≈ 3.4 mmHg
This means that our experiment can reliably detect a difference in mean blood pressure of at least 3.4 mmHg between the two groups.
Method 2: Using Online Calculators and Software

There are several online calculators and software programs available that can calculate the MDE for you. Some popular options include G*Power, SAS, and R. These tools can save time and reduce errors, but it's essential to understand the underlying formulas and assumptions to interpret the results correctly.
Example:
Using G*Power, we can calculate the MDE for the same experiment as above:
- Enter the desired power (80%), significance level (0.05), and sample size (100)
- Select the "Means: Difference between two independent means" test
- Click "Calculate"
G*Power outputs the MDE as approximately 3.4 mmHg, which matches our calculation using the formula.
Method 3: Using Simulation-Based Methods

Simulation-based methods involve generating simulated data to estimate the MDE. This approach can be useful when the underlying distribution of the data is complex or unknown.
Example:
We can use R to simulate data from a normal distribution with a mean difference of 3.4 mmHg and a standard deviation of 10 mmHg. We can then calculate the proportion of simulations that result in a statistically significant difference (p < 0.05) using a t-test.
Using this approach, we can estimate the MDE as the mean difference that corresponds to a power of 80%.
Method 4: Using Pilot Data
If pilot data are available, we can estimate the MDE using the standard deviation and mean difference observed in the pilot study.
Example:
Suppose we have pilot data from a study with 20 participants per group, which showed a mean difference of 4.2 mmHg and a standard deviation of 12 mmHg. We can estimate the MDE using the formula:
MDE = (Zα + Zβ)^2 * σ^2 / n
where n is the sample size of the pilot study.
MDE ≈ (1.96 + 0.842)^2 * 12^2 / 20 ≈ 4.8 mmHg
Method 5: Using Historical Data

If historical data are available, we can estimate the MDE using the standard deviation and mean difference observed in previous studies.
Example:
Suppose we have data from a previous study with 50 participants per group, which showed a mean difference of 3.1 mmHg and a standard deviation of 10 mmHg. We can estimate the MDE using the formula:
MDE = (Zα + Zβ)^2 * σ^2 / n
where n is the sample size of the previous study.
MDE ≈ (1.96 + 0.842)^2 * 10^2 / 50 ≈ 2.6 mmHg
Method 6: Using Expert Opinion

In some cases, expert opinion may be the only available information to estimate the MDE.
Example:
Suppose we consult with a clinician who believes that a difference in mean blood pressure of at least 5 mmHg is clinically meaningful. We can use this value as an estimate of the MDE.
Method 7: Using a Combination of Methods
In many cases, it's possible to use a combination of methods to estimate the MDE.
Example:
Suppose we use a combination of historical data and expert opinion to estimate the MDE. We can calculate the MDE using the formula:
MDE = (Zα + Zβ)^2 * σ^2 / n
where n is the sample size of the historical study, and then adjust this value based on expert opinion.
Minimum Detectable Effect Image Gallery
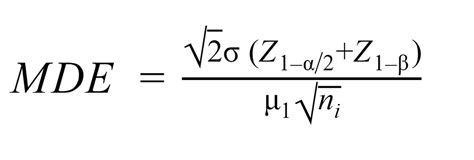



We encourage you to share your experiences and challenges in calculating the Minimum Detectable Effect in the comments section below. How do you estimate the MDE in your studies? What methods do you find most reliable? Share your thoughts and let's continue the conversation!
