Master Normal Distributions With 7 Essential Worksheet Tips

Understanding normal distributions is a fundamental concept in statistics, and mastering it can be a game-changer for students, researchers, and professionals alike. One effective way to grasp this concept is through practice with worksheets. In this article, we will explore seven essential worksheet tips to help you master normal distributions.

The Importance of Normal Distributions

Normal distributions, also known as Gaussian distributions or bell curves, are a type of probability distribution that is symmetric about the mean and has a specific shape. They are widely used in statistics, engineering, economics, and social sciences to model real-world phenomena, such as heights, weights, and IQ scores.

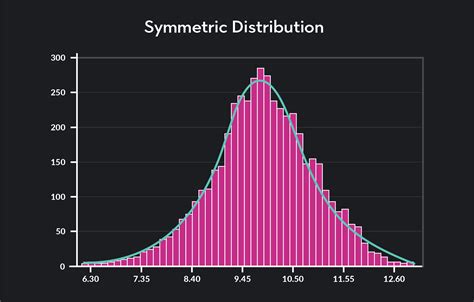
Why Practice with Worksheets is Essential

While understanding the theoretical concepts of normal distributions is crucial, practice is equally important. Worksheets provide a hands-on approach to learning, allowing you to apply theoretical concepts to real-world problems. By practicing with worksheets, you can develop your problem-solving skills, identify areas where you need improvement, and build confidence in your ability to work with normal distributions.

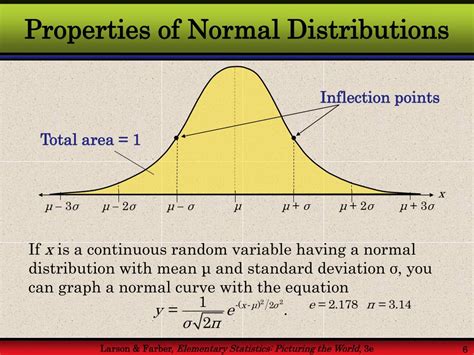
Tip 1: Understand the Properties of Normal Distributions

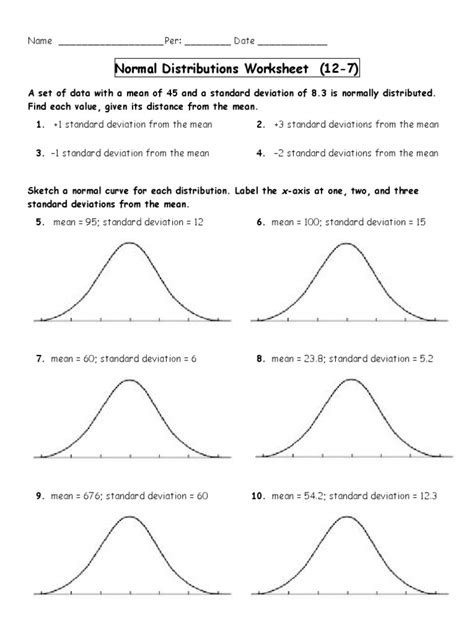
Before diving into worksheets, it's essential to understand the properties of normal distributions. A normal distribution is characterized by its mean (μ), standard deviation (σ), and the fact that it is symmetric about the mean. The mean, median, and mode are all equal in a normal distribution. Understanding these properties will help you navigate worksheets more effectively.

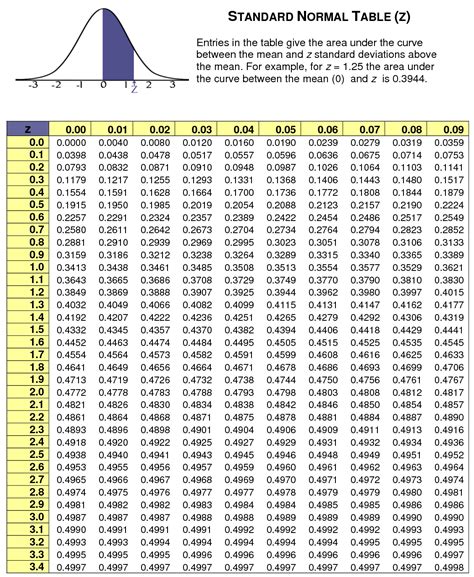
Tip 2: Learn to Calculate z-Scores

z-Scores are a crucial concept in normal distributions, and learning to calculate them is essential. A z-score indicates how many standard deviations an element is from the mean. The formula to calculate a z-score is:

z = (X - μ) / σ

where X is the element, μ is the mean, and σ is the standard deviation.

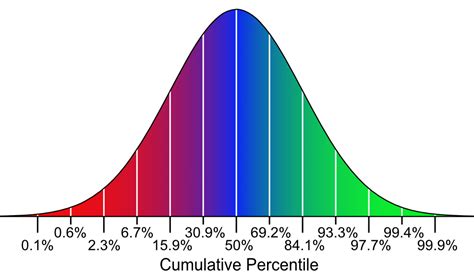
Tip 3: Practice Finding Percentiles and Quartiles

Percentiles and quartiles are important concepts in normal distributions. Percentiles divide the distribution into 100 equal parts, while quartiles divide it into 4 equal parts. Practicing finding percentiles and quartiles will help you understand how to work with normal distributions.

Tip 4: Learn to Create Normal Distribution Graphs

Creating normal distribution graphs is an essential skill to master. By plotting the distribution, you can visualize the data and understand the relationships between the mean, standard deviation, and percentiles.

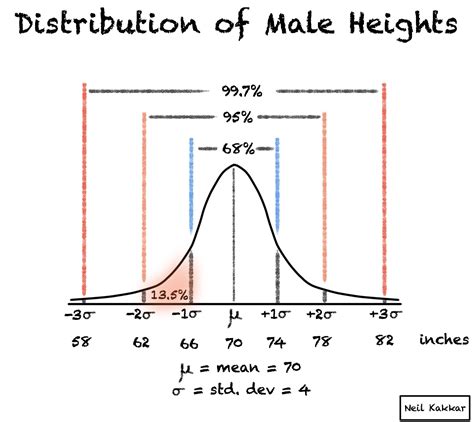
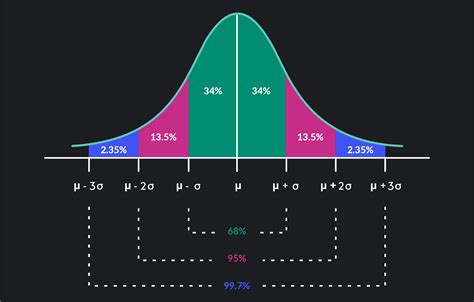
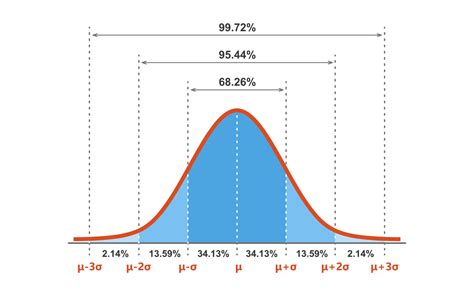
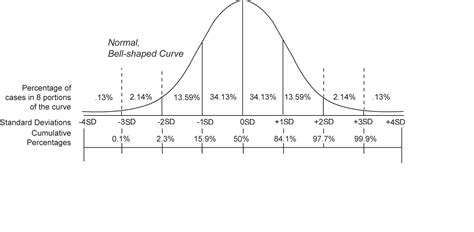
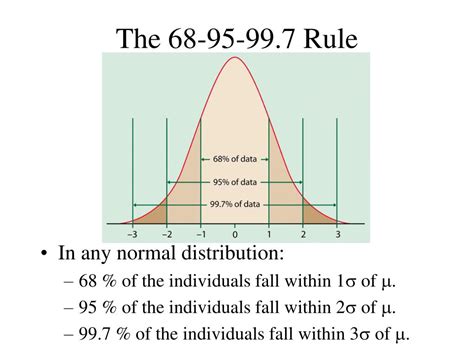
Tip 5: Understand the 68-95-99.7 Rule

The 68-95-99.7 rule, also known as the empirical rule, states that about 68% of the data falls within 1 standard deviation of the mean, about 95% falls within 2 standard deviations, and about 99.7% falls within 3 standard deviations. Understanding this rule will help you estimate the spread of the data.

Tip 6: Practice with Real-World Examples

Practicing with real-world examples will help you apply theoretical concepts to practical problems. Try to find worksheets that include real-world examples, such as heights, weights, or IQ scores.

Tip 7: Check Your Answers and Reflect

Finally, it's essential to check your answers and reflect on your mistakes. This will help you identify areas where you need improvement and build confidence in your ability to work with normal distributions.

Gallery of Normal Distribution Images

Normal Distribution Image Gallery

Conclusion

Mastering normal distributions is a crucial skill in statistics, and practicing with worksheets is an effective way to achieve this. By following these seven essential worksheet tips, you can develop your problem-solving skills, identify areas where you need improvement, and build confidence in your ability to work with normal distributions. Remember to practice regularly, check your answers, and reflect on your mistakes. With persistence and dedication, you can become proficient in working with normal distributions.