Intro
Unlock the secrets of permutations and combinations with our comprehensive worksheet answers. Dive into the world of probability and statistics, exploring essential concepts and formulas. Master the art of arranging objects, calculating possibilities, and understanding probability distributions with our expert solutions.
Understanding the Fundamentals of Permutations and Combinations

Permutations and combinations are essential concepts in mathematics, particularly in algebra and statistics. These concepts are used to calculate the number of ways to arrange objects in a specific order or to select objects from a larger set. Understanding permutations and combinations is crucial for solving problems in various fields, including mathematics, science, engineering, and finance.
In this article, we will explore the fundamental principles of permutations and combinations, provide examples, and offer a worksheet with answers to help you practice and reinforce your understanding of these concepts.
What are Permutations?
A permutation is an arrangement of objects in a specific order. For example, if you have three letters, A, B, and C, the permutations of these letters are ABC, ACB, BAC, BCA, CAB, and CBA. The order of the letters matters, so ABC and BCA are considered different permutations.
Permutation Formula

The permutation formula is used to calculate the number of permutations of a set of objects. The formula is:
n! / (n-r)!
where n is the total number of objects, r is the number of objects being chosen, and! denotes the factorial.
For example, if you have 5 objects and you want to choose 3, the permutation formula would be:
5! / (5-3)! = 5! / 2! = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 120 / 2 = 60
So, there are 60 permutations of 5 objects taken 3 at a time.
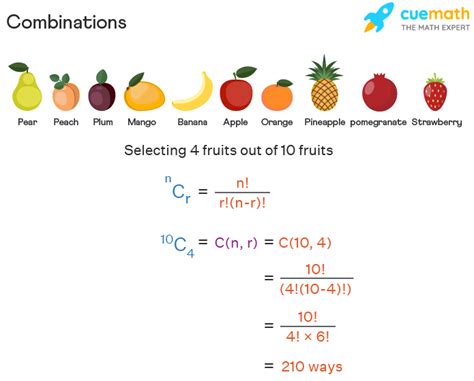
What are Combinations?
A combination is a selection of objects from a larger set, without regard to order. For example, if you have three letters, A, B, and C, the combinations of these letters are AB, AC, and BC. The order of the letters does not matter, so AB and BA are considered the same combination.
Combination Formula
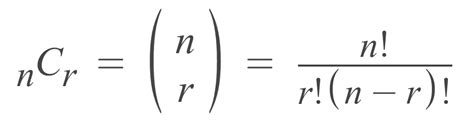
The combination formula is used to calculate the number of combinations of a set of objects. The formula is:
n! / (r! × (n-r)!)
where n is the total number of objects, r is the number of objects being chosen, and! denotes the factorial.
For example, if you have 5 objects and you want to choose 3, the combination formula would be:
5! / (3! × (5-3)!) = 5! / (3! × 2!) = (5 × 4 × 3 × 2 × 1) / ((3 × 2 × 1) × (2 × 1)) = 120 / (6 × 2) = 120 / 12 = 10
So, there are 10 combinations of 5 objects taken 3 at a time.
Permutations and Combinations Worksheet Answers
Here are 7 essential permutations and combinations problems, along with the answers:
- How many permutations of the letters A, B, and C are there?
Answer: 6 (ABC, ACB, BAC, BCA, CAB, and CBA)
- How many combinations of the letters A, B, and C are there?
Answer: 3 (AB, AC, and BC)
- A pizza parlor offers 5 toppings. How many permutations of 3 toppings are there?
Answer: 60 (using the permutation formula)
- A bookshelf has 5 books. How many combinations of 3 books are there?
Answer: 10 (using the combination formula)
- How many permutations of the numbers 1, 2, and 3 are there?
Answer: 6 (123, 132, 213, 231, 312, and 321)
- A committee has 5 members. How many combinations of 2 members are there?
Answer: 10 (using the combination formula)
- A deck of cards has 52 cards. How many permutations of 5 cards are there?
Answer: 2,598,960 (using the permutation formula)
Conclusion
Permutations and combinations are essential concepts in mathematics, and understanding these concepts is crucial for solving problems in various fields. The permutation formula and combination formula can be used to calculate the number of permutations and combinations of a set of objects. By practicing with the worksheet answers provided, you can reinforce your understanding of these concepts and become proficient in solving permutation and combination problems.
Permutations and Combinations Image Gallery