Unlock Pi Chart Trigonometry Basics, exploring circular functions, radians, and trigonometric ratios to master sine, cosine, and tangent calculations.
Understanding the basics of trigonometry is crucial for various fields, including mathematics, physics, engineering, and more. At the heart of trigonometry lies the pi chart, a fundamental tool used to calculate and visualize the relationships between the sides and angles of triangles. In this article, we will delve into the world of pi chart trigonometry basics, exploring its importance, key concepts, and practical applications.
The study of trigonometry dates back to ancient civilizations, with evidence of its use found in the works of Greek mathematicians such as Euclid and Archimedes. Over time, trigonometry has evolved to become a vital component of modern mathematics and science. The pi chart, a circular representation of the unit circle, is a cornerstone of trigonometry, allowing us to calculate trigonometric functions such as sine, cosine, and tangent.
The pi chart is a powerful tool that helps us understand the relationships between angles and their corresponding trigonometric values. By using the pi chart, we can easily identify patterns and connections between different angles, making it an essential resource for problem-solving and critical thinking. In addition, the pi chart is widely used in various fields, including navigation, physics, engineering, and computer science, making it a fundamental concept that transcends academic boundaries.
Introduction to Pi Chart Trigonometry
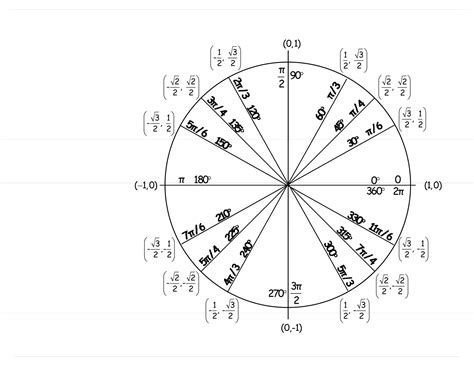
To begin our exploration of pi chart trigonometry basics, let's start with the fundamental concepts. The pi chart is a circular representation of the unit circle, with the radius equal to 1. The circle is divided into four quadrants, each representing a different range of angles. The angles are measured in radians, with the radian measure of an angle equal to the length of the arc subtended by the angle at the center of the circle.
Key Concepts in Pi Chart Trigonometry
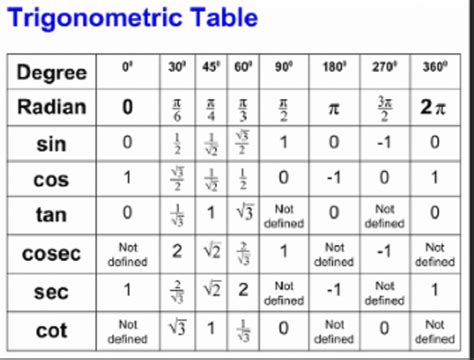
The pi chart is based on several key concepts, including: * The unit circle: a circle with a radius of 1, used to define the trigonometric functions. * Radian measure: a way of measuring angles in terms of the length of the arc subtended by the angle at the center of the circle. * Trigonometric functions: relationships between the sides and angles of triangles, including sine, cosine, and tangent. * Quadrants: the four regions of the pi chart, each representing a different range of angles.Understanding Trigonometric Functions

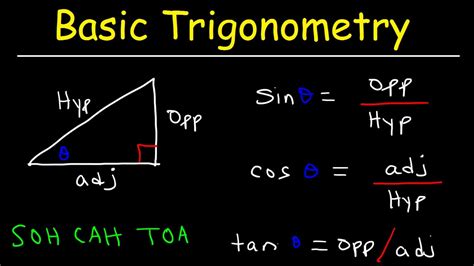
Trigonometric functions are the foundation of pi chart trigonometry basics. The three primary trigonometric functions are:
- Sine (sin): the ratio of the length of the side opposite an angle to the length of the hypotenuse.
- Cosine (cos): the ratio of the length of the side adjacent to an angle to the length of the hypotenuse.
- Tangent (tan): the ratio of the length of the side opposite an angle to the length of the side adjacent to the angle.
These functions can be used to calculate the lengths of sides and angles in triangles, making them essential tools for problem-solving in mathematics and science.
Practical Applications of Pi Chart Trigonometry
Pi chart trigonometry basics have numerous practical applications in various fields, including: * Navigation: trigonometry is used to calculate distances, directions, and positions in navigation systems. * Physics: trigonometry is used to describe the motion of objects, including projectiles and oscillations. * Engineering: trigonometry is used to design and analyze structures, including bridges and buildings. * Computer science: trigonometry is used in computer graphics, game development, and scientific simulations.Calculating Trigonometric Values
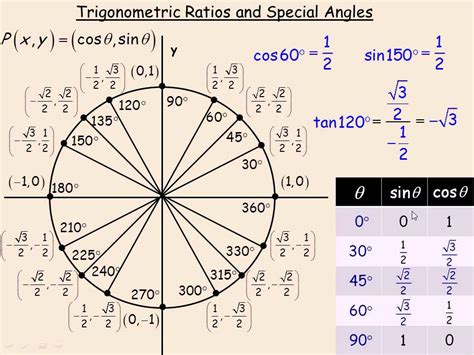
To calculate trigonometric values using the pi chart, we need to understand the relationships between the angles and their corresponding trigonometric values. The pi chart provides a visual representation of these relationships, allowing us to easily identify patterns and connections between different angles.
Here are the steps to calculate trigonometric values using the pi chart:
- Identify the angle: determine the angle for which you want to calculate the trigonometric value.
- Locate the angle on the pi chart: find the angle on the pi chart and identify the corresponding point on the unit circle.
- Determine the trigonometric value: use the coordinates of the point to calculate the trigonometric value.
Common Trigonometric Identities
Trigonometric identities are equations that relate different trigonometric functions. Here are some common trigonometric identities: * Pythagorean identity: sin^2(x) + cos^2(x) = 1 * Sum and difference identities: sin(a + b) = sin(a)cos(b) + cos(a)sin(b), cos(a + b) = cos(a)cos(b) - sin(a)sin(b) * Double-angle identities: sin(2x) = 2sin(x)cos(x), cos(2x) = 2cos^2(x) - 1Real-World Applications of Pi Chart Trigonometry

Pi chart trigonometry basics have numerous real-world applications, including:
- Navigation systems: trigonometry is used to calculate distances, directions, and positions in navigation systems, such as GPS.
- Medical imaging: trigonometry is used in medical imaging techniques, such as MRI and CT scans, to reconstruct images of the body.
- Computer graphics: trigonometry is used in computer graphics to create 3D models and animations.
- Scientific simulations: trigonometry is used in scientific simulations, such as climate modeling and fluid dynamics, to model complex systems.
Benefits of Studying Pi Chart Trigonometry
Studying pi chart trigonometry basics has numerous benefits, including: * Improved problem-solving skills: trigonometry helps develop critical thinking and problem-solving skills. * Enhanced understanding of mathematics and science: trigonometry provides a deeper understanding of mathematical and scientific concepts. * Increased career opportunities: trigonometry is used in various fields, including engineering, physics, and computer science, making it a valuable skill for career advancement.Gallery of Pi Chart Trigonometry
Pi Chart Trigonometry Image Gallery

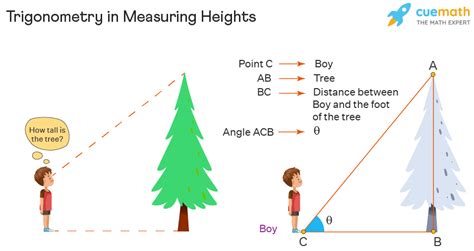
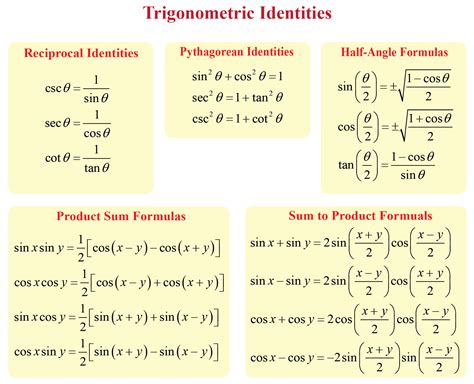

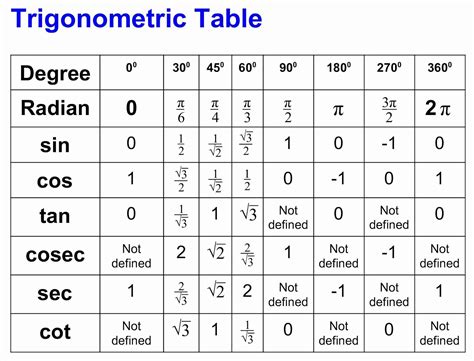
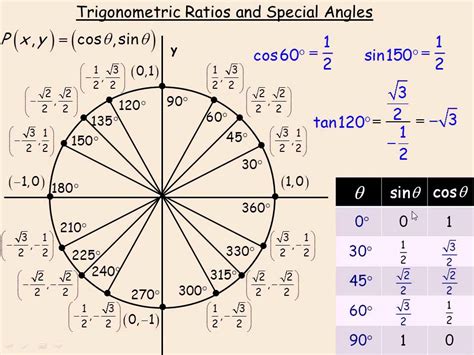

Final Thoughts on Pi Chart Trigonometry

In conclusion, pi chart trigonometry basics are a fundamental concept in mathematics and science, with numerous practical applications in various fields. By understanding the relationships between angles and their corresponding trigonometric values, we can develop critical thinking and problem-solving skills, enhance our understanding of mathematical and scientific concepts, and increase our career opportunities. We hope this article has provided you with a comprehensive overview of pi chart trigonometry basics and inspired you to explore this fascinating topic further. If you have any questions or comments, please don't hesitate to share them with us. Additionally, we encourage you to share this article with others who may be interested in learning more about pi chart trigonometry basics.
