5 Steps To Principal Component Analysis In Excel

Principal Component Analysis (PCA) is a widely used statistical technique in data analysis and machine learning. It is a dimensionality reduction method that transforms a set of correlated variables into a new set of uncorrelated variables, called principal components. In this article, we will explore the 5 steps to perform Principal Component Analysis in Excel.

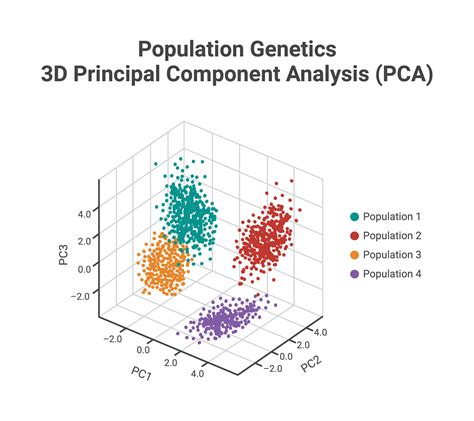
Understanding Principal Component Analysis

Before we dive into the steps, it's essential to understand the basics of Principal Component Analysis. PCA is a technique used to reduce the dimensionality of a dataset while retaining most of the information. It works by identifying the directions of maximum variance in the data and projecting the data onto those directions.

Why Use Principal Component Analysis?

PCA has several benefits, including:

• Reducing the dimensionality of a dataset, making it easier to visualize and analyze
• Identifying patterns and relationships in the data that may not be apparent through other methods
• Improving the performance of machine learning models by reducing the impact of correlated variables

Step 1: Prepare Your Data

The first step in performing PCA in Excel is to prepare your data. This involves:

• Ensuring that your data is in a suitable format for analysis
• Checking for missing values and outliers
• Normalizing or scaling the data to ensure that all variables are on the same scale

Tips for Preparing Your Data

• Use the Excel functions =AVERAGE() and =STDEV() to calculate the mean and standard deviation of each variable
• Use the Excel function =NORM.S.DIST() to normalize the data
• Use the Excel function =IFERROR() to replace missing values with a suitable value (e.g., the mean or median)

Step 2: Calculate the Covariance Matrix

The second step in performing PCA in Excel is to calculate the covariance matrix. This involves:

• Calculating the covariance between each pair of variables
• Creating a matrix of the covariances

Tips for Calculating the Covariance Matrix

• Use the Excel function =COVAR() to calculate the covariance between each pair of variables
• Use the Excel function =MMULT() to create the covariance matrix

Step 3: Calculate the Eigenvectors and Eigenvalues

The third step in performing PCA in Excel is to calculate the eigenvectors and eigenvalues. This involves:

• Calculating the eigenvectors and eigenvalues of the covariance matrix
• Selecting the top k eigenvectors (where k is the number of principal components you want to retain)

Tips for Calculating the Eigenvectors and Eigenvalues

• Use the Excel function =EIGENVALUES() to calculate the eigenvalues
• Use the Excel function =EIGENVECTORS() to calculate the eigenvectors
• Use the Excel function =INDEX() to select the top k eigenvectors

Step 4: Transform the Data

The fourth step in performing PCA in Excel is to transform the data. This involves:

• Projecting the original data onto the new axes defined by the eigenvectors
• Creating a new dataset with the transformed data

Tips for Transforming the Data

• Use the Excel function =MMULT() to project the data onto the new axes
• Use the Excel function =INDEX() to create the new dataset

Step 5: Interpret the Results

The final step in performing PCA in Excel is to interpret the results. This involves:

• Analyzing the transformed data to identify patterns and relationships
• Using the loadings to identify the most important variables

Tips for Interpreting the Results

• Use the Excel function =SUMIFS() to calculate the loadings
• Use the Excel function =INDEX() to identify the most important variables

Principal Component Analysis Image Gallery

We hope this article has provided a comprehensive guide to performing Principal Component Analysis in Excel. By following these 5 steps, you can reduce the dimensionality of your dataset and identify patterns and relationships that may not be apparent through other methods. Remember to interpret the results carefully and use the loadings to identify the most important variables. Happy analyzing!