Quadratic Regression In Excel Made Easy

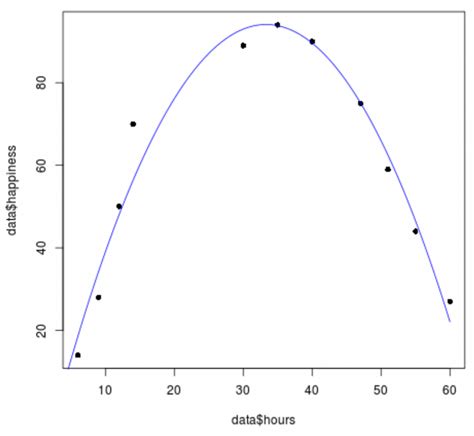
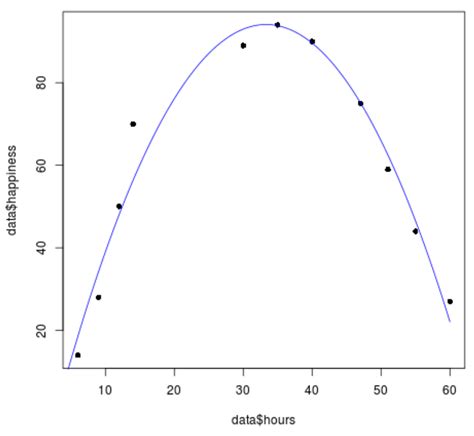
Quadratic regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. In quadratic regression, the relationship between the variables is modeled using a quadratic equation, which is a polynomial equation of degree two. This type of regression is useful when the relationship between the variables is non-linear, but still relatively smooth and continuous.

Quadratic regression is commonly used in various fields, including economics, finance, engineering, and social sciences. For instance, it can be used to model the relationship between the price of a product and its demand, or the relationship between the dosage of a medication and its effect on patients.

In this article, we will discuss how to perform quadratic regression in Excel, a popular spreadsheet software. We will cover the basics of quadratic regression, including the equation, the assumptions, and the steps involved in performing the analysis. We will also provide a step-by-step guide on how to perform quadratic regression in Excel, using the built-in functions and tools.

What is Quadratic Regression?

Quadratic regression is a type of regression analysis that models the relationship between a dependent variable and one or more independent variables using a quadratic equation. The quadratic equation is a polynomial equation of degree two, which means it includes a squared term.

The general form of a quadratic equation is:

y = a + bx + cx^2 + ε

where:

• y is the dependent variable
• x is the independent variable
• a is the intercept or constant term
• b is the coefficient of the linear term
• c is the coefficient of the quadratic term
• ε is the error term

Assumptions of Quadratic Regression

Like other regression models, quadratic regression assumes that the relationship between the variables is linear in the parameters, and that the errors are normally distributed with a mean of zero and a constant variance.

Additionally, quadratic regression assumes that the relationship between the variables is smooth and continuous, and that the quadratic term is not too large compared to the linear term.

Steps Involved in Quadratic Regression

Performing quadratic regression involves several steps, including:

1. Data preparation: Collect and prepare the data, including the dependent and independent variables.
2. Model specification: Specify the quadratic equation, including the intercept, linear term, and quadratic term.
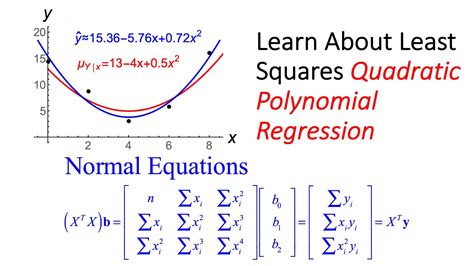
3. Estimation: Estimate the coefficients of the quadratic equation using a suitable method, such as ordinary least squares (OLS).
4. Diagnosis: Diagnose the model to check for any issues, such as multicollinearity, heteroscedasticity, and non-normality.
5. Interpretation: Interpret the results, including the coefficients, R-squared, and p-values.

Performing Quadratic Regression in Excel

Excel provides several built-in functions and tools for performing quadratic regression. Here are the steps involved:

1. Enter the data: Enter the data, including the dependent and independent variables, into an Excel spreadsheet.
2. Use the TREND function: Use the TREND function to estimate the coefficients of the quadratic equation.

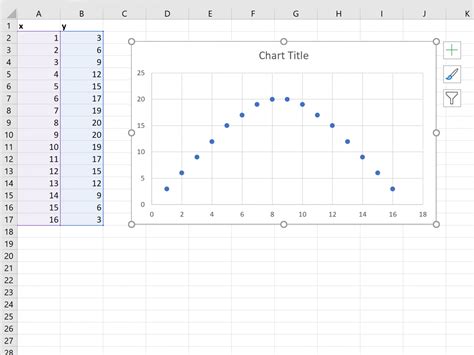
The TREND function takes several arguments, including the array of x-values, the array of y-values, and the order of the polynomial.

Using the TREND function

The TREND function can be used to estimate the coefficients of the quadratic equation. Here is an example:

=TREND(B2:B10, A2:A10, 2)

This formula estimates the coefficients of a quadratic equation using the data in cells A2:A10 and B2:B10.

Using the LINEST function

The LINEST function can also be used to estimate the coefficients of the quadratic equation. Here is an example:

=LINEST(B2:B10, A2:A10^2, TRUE, TRUE)

This formula estimates the coefficients of a quadratic equation using the data in cells A2:A10 and B2:B10.

Interpreting the Results

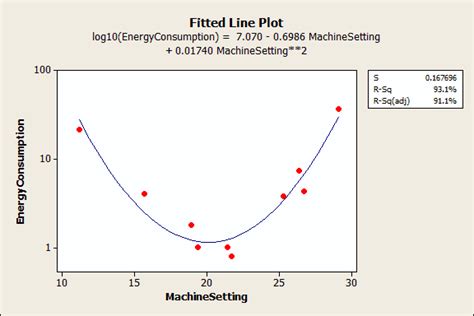
The results of the quadratic regression analysis can be interpreted using the coefficients, R-squared, and p-values.

The coefficients of the quadratic equation can be used to predict the value of the dependent variable for a given value of the independent variable.

The R-squared value measures the goodness of fit of the model, with higher values indicating a better fit.

The p-values can be used to test the significance of the coefficients and the overall model.

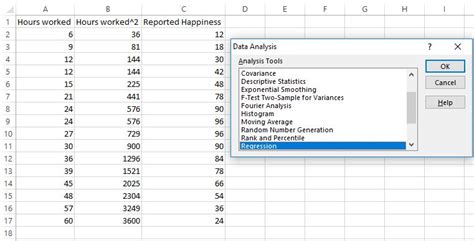
Gallery of Quadratic Regression Images

Quadratic Regression Image Gallery

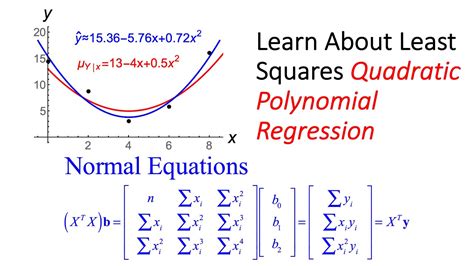
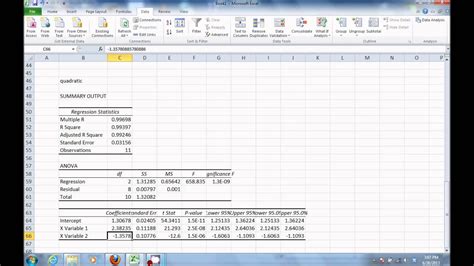
We hope this article has provided a comprehensive guide to performing quadratic regression in Excel. If you have any questions or need further clarification, please don't hesitate to ask.